Supervised Learning

Applications in which the training data comprises examples of the input vectors along with their corresponding target vectors are known as supervised learning problems[1]. The training data consists of a set of training examples. In supervised learning, each example is a pair consisting of an input object(typically a vector) and a desired output value (also called the supervisory signal).For instance, a training example in neural network could be like this,

, where $//<![CDATA[ \begin{array}{l}\vec{x}_i\end{array} //]]>$ is the $//<![CDATA[ \begin{array}{l}i^{th}\end{array} //]]>$ input vector and correspondingly $//<![CDATA[ \begin{array}{l}\vec{y}_i\end{array} //]]>$ is the desired $//<![CDATA[ \begin{array}{l}i^{th}\end{array} //]]>$ output vector.

Error Measures

What we'd like during learning process is an algorithm which let us find weights and biases so that the output from the network $//<![CDATA[ \begin{array}{l}\vec{f}(\vec{x}_i)\end{array} //]]>$ approximates $//<![CDATA[ \begin{array}{l}\vec{y}_i\end{array} //]]>$ for all training inputs $//<![CDATA[ \begin{array}{l}\vec{x}_i\end{array} //]]>$. To quantify how well we're achieving this goal we should use a method to measure the error which indicates the difference between $//<![CDATA[ \begin{array}{l}\vec{f}(\vec{x}_i)\end{array} //]]>$ and $//<![CDATA[ \begin{array}{l}\vec{y}_i\end{array} //]]>$(also called cost function). A widely used method is the Mean Squared Errors(MSE):

Here, $//<![CDATA[ \begin{array}{l}w\end{array} //]]>$  denotes the collection of all weights in the network, $//<![CDATA[ \begin{array}{l}b\end{array} //]]>$ all the biases, $//<![CDATA[ \begin{array}{l}n\end{array} //]]>$ is the total number of training inputs, $//<![CDATA[ \begin{array}{l}\vec{f}(\vec{x})\end{array} //]]>$ is the vector of outputs from the network when $//<![CDATA[ \begin{array}{l}\vec{x}\end{array} //]]>$ is the input, $//<![CDATA[ \begin{array}{l}\vec{y}\end{array} //]]>$ is the desired output, and the sum is over all training inputs, $//<![CDATA[ \begin{array}{l}\vec{x}\end{array} //]]>$.

Besides the MSE, the cross-entropy error measure is also used in neural networks:

 where $//<![CDATA[ \begin{array}{l}n\end{array} //]]>$ is the total number of items of training data, the sum over all training inputs, $//<![CDATA[ \begin{array}{l}\vec{x}\end{array} //]]>$, and  $//<![CDATA[ \begin{array}{l}\vec{y}\end{array} //]]>$ is the corresponding desired output.

Training Protocols

Here, we mainly introduce four protocols:

• Batch training: batch training computes the gradient of the cost function w.r.t. to the parameters$//<![CDATA[ \begin{array}{l}(w,b)\end{array} //]]>$ for the entire training dataset.
• Stochastic training: Stochastic training in contrast performs a parameter update for each training example $//<![CDATA[ \begin{array}{l}\vec{x}_i\end{array} //]]>$ and desired output $//<![CDATA[ \begin{array}{l}\vec{y}_i\end{array} //]]>$.
• Online training: In this protocol, each training data would be used only once to update the weights and biases.
• Mini-batch training: stochastic training works by randomly picking out a small number $//<![CDATA[ \begin{array}{l}m\end{array} //]]>$ of randomly chosen training inputs. We'll refer each of those random training inputs as a mini-batch. It takes the best of all the three training protocols and performs an update for every mini-batch of $//<![CDATA[ \begin{array}{l}n\end{array} //]]>$ training examples.

Parameter Optimization

Recapping, our goal in training a neural network is to find weights and biases which minimize the cost function $//<![CDATA[ \begin{array}{l}E(w,b)\end{array} //]]>$, which we could also call Parameter Optimization.
Let's first consider the simplest situation:$//<![CDATA[ \begin{array}{l}E(\theta_1,\theta_2) = g(\theta_1,\theta_2)\end{array} //]]>$, where $//<![CDATA[ \begin{array}{l}\theta_1\end{array} //]]>$ and $//<![CDATA[ \begin{array}{l}\theta_2\end{array} //]]>$ are 1-dimensional variables. Assume that $//<![CDATA[ \begin{array}{l}E(\theta_1,\theta_2)\end{array} //]]>$ has the form:

         Fig. 1: Function $//<![CDATA[ \begin{array}{l}E(\theta_1,\theta_2)\end{array} //]]>$.(Source:2)

In Figure, what we'd like is to find where $//<![CDATA[ \begin{array}{l}E(\theta_1,\theta_2)\end{array} //]]>$ achieves its global minimum. Now, for the function plotted above, we can eyeball the graph and find the minimum. But actually we do not know where is the exact point at which $//<![CDATA[ \begin{array}{l}E(\theta_1,\theta_2)\end{array} //]]>$ reaches its minimum.
Theoretically, when the minimum of $//<![CDATA[ \begin{array}{l}E(\theta_1,\theta_2)\end{array} //]]>$ is reached, then the following condition should be satisfied:

In practice, the cost function in a neural network is much more complicated so that it could be impossible to calculate the zero point of the derivative of $//<![CDATA[ \begin{array}{l}E(\theta_1,\theta_2)\end{array} //]]>$. Based on this fact, we start by thinking of $//<![CDATA[ \begin{array}{l}E(\theta_1,\theta_2)\end{array} //]]>$ as a kind of valley. Then we image a ball rolling down the slope of the valley and eventually it could roll to the bottom of the valley. So how to use this experience in our neural network?

From Calculus, we knew that:

Recall that our purpose is to minimize the cost function $//<![CDATA[ \begin{array}{l}E(\theta_1,\theta_2)\end{array} //]]>$, so if we choose 

where $//<![CDATA[ \begin{array}{l}\eta\end{array} //]]>$ is the learning rate (a small, positive parameter). Thereby, we can infer from the cost function that 

which guarantees$//<![CDATA[ \begin{array}{l}\Delta E \leq 0\end{array} //]]>$ so that the "ball" could roll to the bottom of the "valley". This method is called Gradient Descent.

Besides this, Newton's Method is also widely used for optimizing the parameters.
Due to the use of second-order information of the cost function in Newton's Method, , the algorithm performs faster convergence.

where $//<![CDATA[ \begin{array}{l}H_n\end{array} //]]>$ is the Hessian matrix of  $//<![CDATA[ \begin{array}{l}E(\vec{\theta})\end{array} //]]>$. The main drawback of this method is its computationally expensive for evaluation and inversion of the Hessian matrix.

Weights Initialization

Now, we've learned how to optimize the parameters. In this subsection, we will see the method to initialize the parameters. But firstly we should clarify if the parameters can all be initialized to zero?
The answer is no, because if every neuron in the network computes the same output, then they will also all compute the same gradients during backpropagation and undergo the exact same parameter updates. In other words, there is no source of asymmetry between neurons if their weights are initialized to be the same.

• Small Random Numbers. As a solution, it is common to initialize the weights of the neurons to small numbers and refer to doing so as symmetry breaking. The idea is that the neurons are all random and unique in the beginning, so they will compute distinct updates and integrate themselves as diverse parts of the full network.
• Calibrating the variances with $//<![CDATA[ \begin{array}{l}1/ \sqrt{n}\end{array} //]]>$. One problem with the above suggestion is that the distribution of the outputs from a randomly initialized neuron has a variance that grows with the number of inputs. It turns out that we can normalize the variance of each neuron’s output to 1 by scaling its weight vector by the square root of its fan-in (i.e. its number of inputs).

Error Backpropagation

In the previous section, we discussed how to initialize and optimize the parameters. Now, let's think more about the optimization of the parameters: How each parameter in a multi-layered neural network be optimized?

Principle Part

To solve this problem, Error Backpropagation Algorithm[2] is the most famous method that is used.This Algorithm comprises of 4 equations.
First, assume the weighted input to the $//<![CDATA[ \begin{array}{l}j_{th}\end{array} //]]>$ neuron in layer $//<![CDATA[ \begin{array}{l}l\end{array} //]]>$  is:

where $//<![CDATA[ \begin{array}{l}a^{l-1}_k\end{array} //]]>$ is the output of the k-th neuron in layer$//<![CDATA[ \begin{array}{l}l-1\end{array} //]]>$ and $//<![CDATA[ \begin{array}{l}w^l_{jk}\end{array} //]]>$ is the corresponding weight.
Next, we define the error $//<![CDATA[ \begin{array}{l}\delta^l_j\end{array} //]]>$ of neuron j in layer $//<![CDATA[ \begin{array}{l}I\end{array} //]]>$ by

• First Equation for Error in the Output Layer, $//<![CDATA[ \begin{array}{l}\delta^L\end{array} //]]>$:

          where $//<![CDATA[ \begin{array}{l}\sigma\end{array} //]]>$ is the activation function.

• Second Function for Error $//<![CDATA[ \begin{array}{l}\delta^l\end{array} //]]>$ in terms of the error in the next layer , $//<![CDATA[ \begin{array}{l}\delta^l+1\end{array} //]]>$:
  
  

  (12)	$$//<![CDATA[ \begin{array}{l}\displaystyle \delta^l = ((w^{l+1})^T \delta^{l+1})\bigodot\sigma'(z^l)\end{array} //]]>$$

  where $//<![CDATA[ \begin{array}{l}\bigodot\end{array} //]]>$ is the Hadamard product.

By combining these two equations above we can compute the error $//<![CDATA[ \begin{array}{l}\delta^l\end{array} //]]>$ for any layer in the network. We start by using First Equation for Error to compute $//<![CDATA[ \begin{array}{l}\delta^L\end{array} //]]>$, then apply the Second Equation for Error to compute $//<![CDATA[ \begin{array}{l}\delta^{L-1}\end{array} //]]>$. Then use the Second Equation for Error  to compute $//<![CDATA[ \begin{array}{l}\delta^{L-2}\end{array} //]]>$, and so on, all the way back through the network.

• Third Equation for the rate of change of the cost with respect to any bias in the network:

   

  (13)	$$//<![CDATA[ \begin{array}{l}\displaystyle \frac{\partial E}{\partial b^l_j} = \delta^l_j\end{array} //]]>$$

  That is, the error $//<![CDATA[ \begin{array}{l}\delta^l_j\end{array} //]]>$ is exactly equal to the rate of change $//<![CDATA[ \begin{array}{l}\frac{\partial E}{\partial b^l_j}\end{array} //]]>$.

• Fourth equation for the rate of change of the cost with respect to any weight in the network:

           This tells us how to compute the partial derivatives $//<![CDATA[ \begin{array}{l}\frac{\partial E}{\partial w^l_{jk}}\end{array} //]]>$ in terms of the quantities $//<![CDATA[ \begin{array}{l}\delta^l\end{array} //]]>$ and $//<![CDATA[ \begin{array}{l}a^{l-1}\end{array} //]]>$, which we already know how to compute.

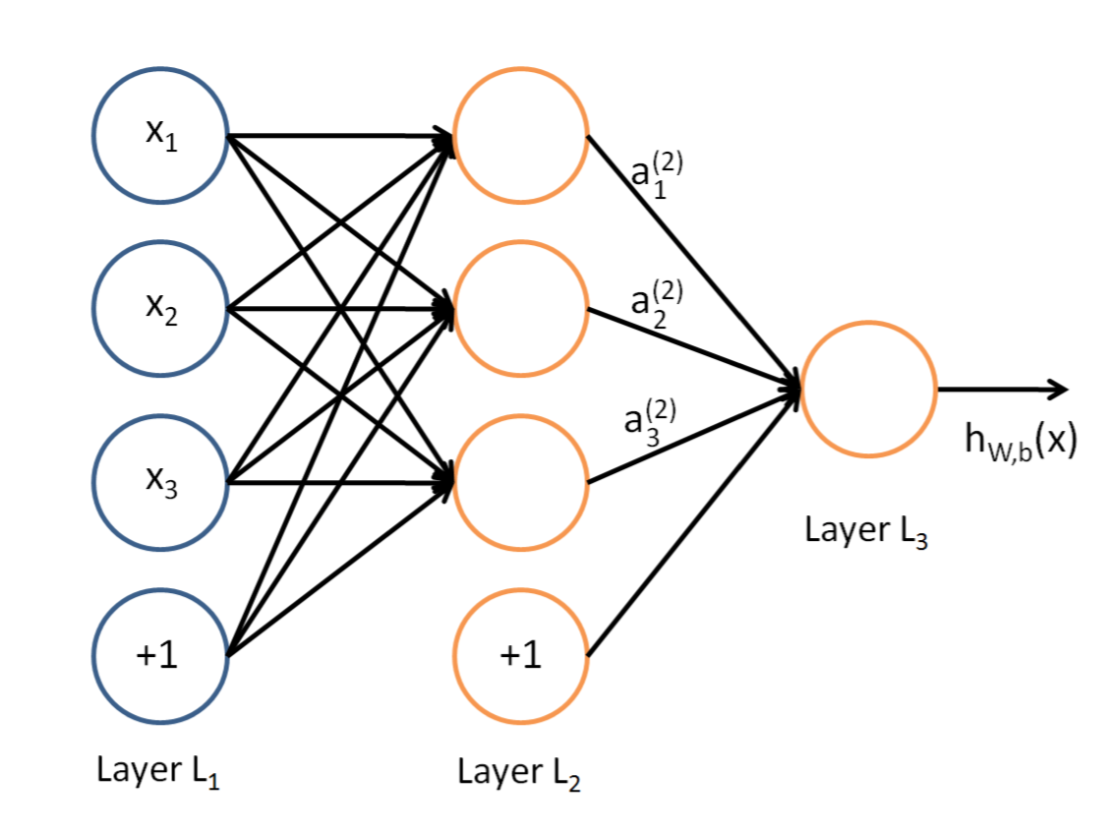
With these four equations, we could "easily" backpropagate the error to each parameter. Here, we only roughly introduced those equations.You may find more about the principle of error backpropagation, here, if you are interested.

Step 1 Forward Propagation

1. Input Layer -----> Hidden Layer:
   First, we calculate the weighted input to the $//<![CDATA[ \begin{array}{l}h_1\end{array} //]]>$ neuron in the hidden layer:

   $$//<![CDATA[ \begin{array}{l}\displaystyle z_{h1} = w_1 * i_1 + w_2 * i_2 + b_1 *1 = 0.3775\end{array} //]]>$$

   The output of the $//<![CDATA[ \begin{array}{l}h_1\end{array} //]]>$ neuron(with the sigmoid activation function) is:

   $$//<![CDATA[ \begin{array}{l}\displaystyle a_{h1} = \frac{1}{1 + e^{- z_{h1} }} = 0.593269992\end{array} //]]>$$

   Similarly, we can get the output of the $//<![CDATA[ \begin{array}{l}h_2\end{array} //]]>$ neuron is:

   $$//<![CDATA[ \begin{array}{l}\displaystyle a_{h2} = 0.596884378\end{array} //]]>$$

2. Hidden Lay ---→ Output Layer:
   Repeat the same procedure from above to the output layer:

    

   $$//<![CDATA[ \begin{array}{l}\displaystyle a_{o1} = \frac{1}{1 + e^{- z_{o1} }} = 0.75136507\end{array} //]]>$$

   $$//<![CDATA[ \begin{array}{l}\displaystyle a_{o2} = \frac{1}{1 + e^{- z_{o2} }} = 0.0.772928465\end{array} //]]>$$

Here, the forward propagation is finished because we have the output of the network with the input and initial parameters we gave. Apparently, the output value $//<![CDATA[ \begin{array}{l}(0.75136079, 0.772928465)\end{array} //]]>$ differs quite far from the desired output value$//<![CDATA[ \begin{array}{l}(0.01,0.99)\end{array} //]]>$. So,we need to apply the back propagation algorithm to the network to update the parameters and re-calculate output.

Step 2 Back propagation

1.   Calculate the error(MSE):
From the first subsection, we knew that:

According to the equation above, we can easily calculate the output of the MSE:

Let's calculate the value of each part from the equation above one by one:

• $//<![CDATA[ \begin{array}{l}\frac{\partial E}{\partial a_{o1}}\end{array} //]]>$： 

  $$//<![CDATA[ \begin{array}{l}\displaystyle E(w,b) = \frac{1}{n} \varSigma_{\vec{x}}||\vec{y}- \vec{f}(\vec{x}) ||^2\end{array} //]]>$$

  $$//<![CDATA[ \begin{array}{l}\displaystyle \frac{\partial E}{\partial a_{o1}} = 2 * \frac{1}{2}*(out_1 - o1 )*(-1) + 0 =0.74136507\end{array} //]]>$$

• $//<![CDATA[ \begin{array}{l}\frac{\partial a_{o1}}{\partial z_{o1}}\end{array} //]]>$：

  $$//<![CDATA[ \begin{array}{l}\displaystyle a_{o1} = \frac{1}{1 + e^{- z_{o1} }}\end{array} //]]>$$

  $$//<![CDATA[ \begin{array}{l}\displaystyle \frac{\partial a_{o1}}{\partial z_{o1}} = a_{o1}*(1-a_{o1}) = 0.186815602\end{array} //]]>$$

• $//<![CDATA[ \begin{array}{l}\frac{\partial z_{o1}}{\partial w_5}\end{array} //]]>$：

  $$//<![CDATA[ \begin{array}{l}\displaystyle z_{o1} = w_5 * a_{h1} + w_6*a_{h2} + b_2 *1\end{array} //]]>$$

  $$//<![CDATA[ \begin{array}{l}\displaystyle \frac{\partial z_{o1}}{\partial w_5} = 1*a_{o1} * w_5^0 +0+0 = 0.593269992\end{array} //]]>$$

At last, $//<![CDATA[ \begin{array}{l}\frac{\partial E}{\partial w_5} =0.082167041\end{array} //]]>$.

You may find that we did not use the error variable $//<![CDATA[ \begin{array}{l}\delta\end{array} //]]>$, then why define it?

Actually we did use it. Relying on the previous equation of $//<![CDATA[ \begin{array}{l}\delta\end{array} //]]>$, and based on the calculation above, we can easily derive that:

Then, $//<![CDATA[ \begin{array}{l}\delta\end{array} //]]>$ can be written as:

So, the derivative of MSE in terms of $//<![CDATA[ \begin{array}{l}w_5\end{array} //]]>$ is:

In this part, the last step is to update the value of $//<![CDATA[ \begin{array}{l}w_5\end{array} //]]>$ to make our network "better":

where $//<![CDATA[ \begin{array}{l}\eta\end{array} //]]>$ is the learning rate, we take its value as 0.5 here.

Similarly, $//<![CDATA[ \begin{array}{l}w_6, w_7,w_8\end{array} //]]>$ could be updated to: