Abstract
In this blog post we will discuss the topic: Diffusion Models for Medical Imaging. The diffusion model will be introduced and as DDPM (denoising diffusion probabilistic model) further elaborated. Three papers with different methods based on DDPM applied in different medical image processing scenarios will be presented and compared based on their respective experimental results.
Author: Unbekannter Benutzer (ge63cuz)
Tutor: Yordanka Velikova
1. Introduction
1.1 Problem Statement
Medical images are high dimensional data rich in deformation such as 2D CT and 3D/4D MR images, which need the methods to achieve competitive real-time performance to be processed. It is challenging to preserve the original image details after translation, which is of crucial value for diagnosis, prognosis and treatment selection. In addition to the image quality, fast inference time is also a significant factor for application in time-critical scenarios such as live data quality control and clinical alerting systems.
1.2 State of the art
Over the last few years, with the advances in deep learning approaches, the extensive development of deep learning-based image processing methods have benefited the medical area a lot. When it comes to generative model, VAE (Variational Autoencoder), GANs (Generative Adversarial Networks [21]) are already popular. There are also some more niche options, such as Flow-based Models and so on.
In addition to these, there is another option - Diffusion Model, which is emerging in the field of Generative Model. The two most advanced text-image generator at present - OpenAI's DALL·E 2 [1] and Google's Imagen [2], are both realized based on the diffusion model.
Figure 1. Examples of Imagen text-image
Before the application of diffusion model, GANs are the mainstream tool when it comes to medical image processing and analysis. However, GANs have the possibility to introduce additional artefacts, which are not expected to occur during medical imaging. Therefore, diffusion models emerge and methods based on it with property to preserve the topology features of the source image start to arouse communities' interest and are gradually applied in several directions.
1.3 What is Diffusion?
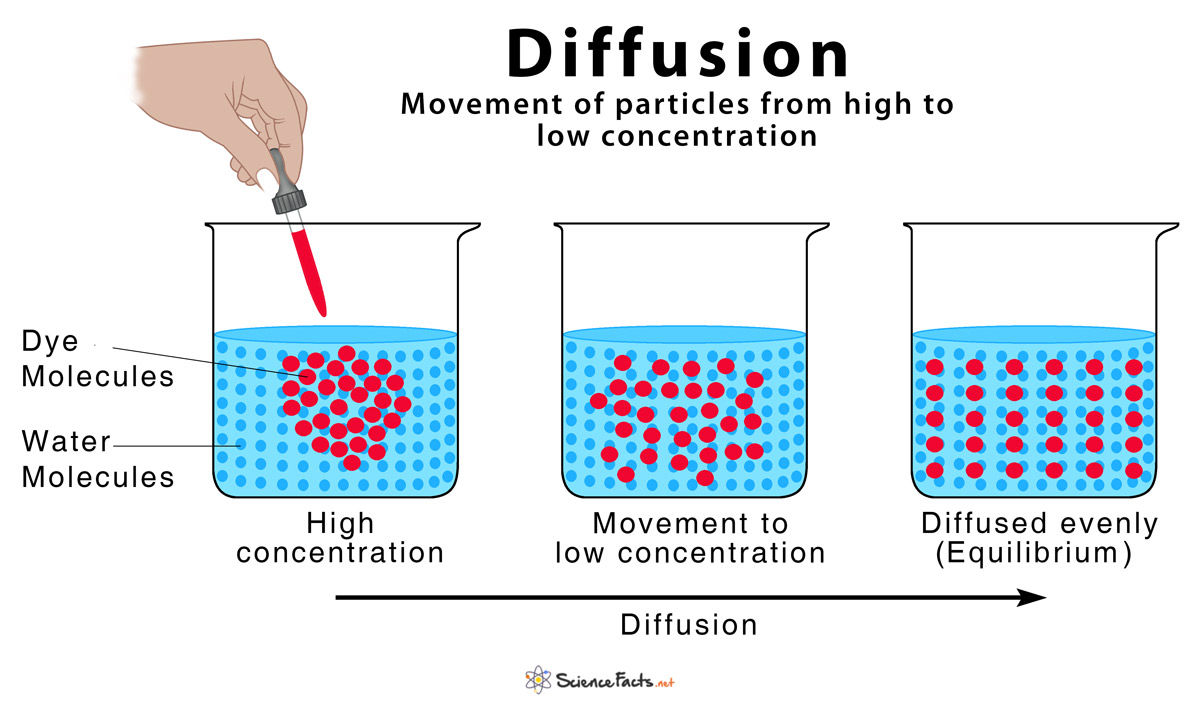
The concept of diffusion is derived from physical thermodynamics, which refers to the movement of particles that diffuse from high concentration to low concentration and finally reach the equilibrium state. Such movement can vividly describe the steps of adding random noise to image in the diffusion model.
Figure 2. Diffusion [5]
1.4 Diffusion Models - DDPM & DDIM
Lately, DDPMs (Denoising Diffusion Probabilistic Models) are in focus for their superiority to surpass GANs on image sythesis [6]. In the flow of this success, DDPMs are also applied on image-to-image translation [7], segmentation [8], reconstruction [9] and registration[10].
Related work:
Today's popularity of generative diffusion models started with the DDPM proposed in a 2020 paper "Denoising Diffusion Probabilistic Models" [3], from which most of the diffusion models currently employed are derived. The mathematical framework of DDPM has already been completed in a ICML2015 paper "Deep Unsupervised Learning using Nonequilibrium Thermodynamics" [4], but DDPM is the first time to implement it on high-resolution image generation, which leads to the later trend.
DDPM simplifies the previous diffusion model [4] and models it through variational inference. This is mainly because the diffusion model is also a latent variable model. Compared with latent variable models such as VAE, the latent variable of the diffusion model is dimensionally the same as the original data, and the inference process (i.e. the diffusion process) is fixed.
The principle of diffusion model:
There are many ways to understand diffusion model, the following introduction is based on DDPM.
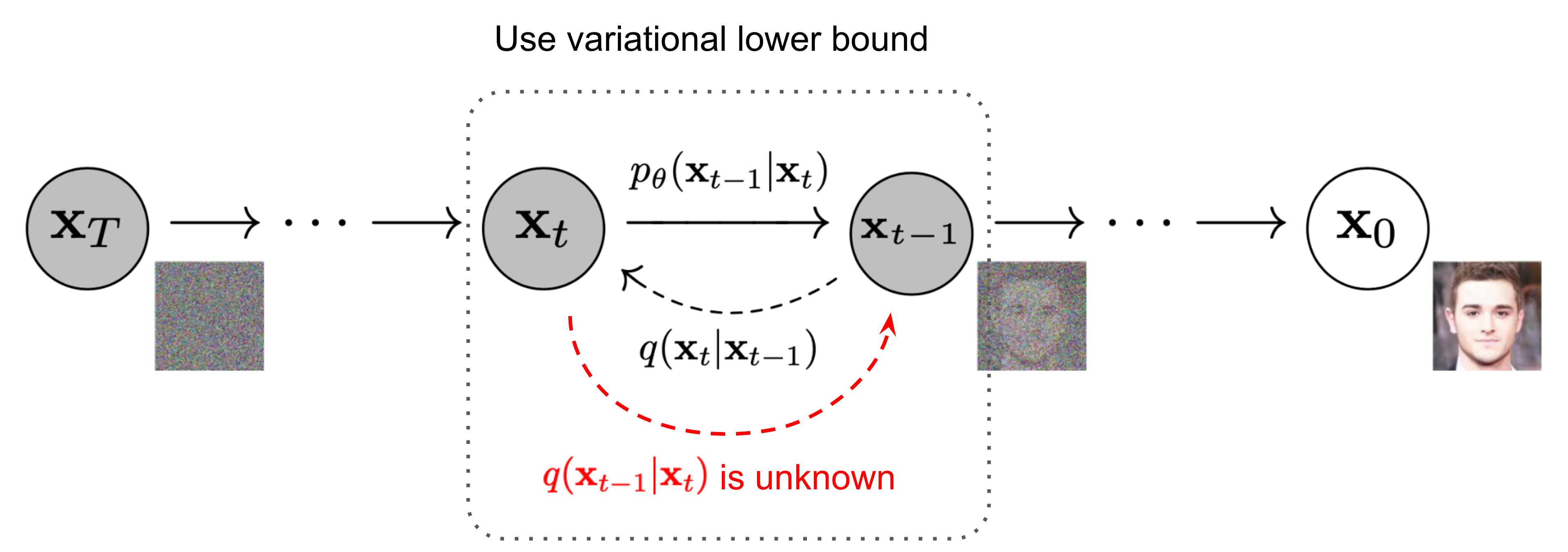
DDPMs are trained to iteratively denoise the input by reversing a forward diffusion process that gradually corrupts it. They are composed of forward process and reverse process.
Forward process (diffusion): the process of adding noise to the image
Given a data point sampled from a real data distribution\mathbf{x}_0 \sim q(\mathbf{x}), in forward process we add small amounts of Gaussian noise to the sample in T timesteps, producing a sequence of noisy sample\mathbf{x}_1, \dots, \mathbf{x}_T. The noise level t of an image xt is steadily increased from 0 to T. The step sizes are controlled by a variance schedule\{\beta_t \in (0, 1)\}_{t=1}^T. The forward noising process q with variances β1, ..., βT is defined by
q(\mathbf{x}_t \vert \mathbf{x}_{t-1}) = \mathcal{N}(\mathbf{x}_t; \sqrt{1 - \beta_t} \mathbf{x}_{t-1}, \beta_t\mathbf{I}) \quad(1)
The data sample x0 gradually loses its distinguishable features as the step t becomes larger. Eventually whenT \to \infty, xT is equivalent to an isotropic Gaussian distribution.
Figure 3. The Markov chain of forward (reverse) process of generating a sample by gradually adding (removing) noise [3].
An important property of the above process is that xt at any arbitrary time step t can be represented by x0 and β in a closed form using reparameterization trick. Let\alpha_t = 1 - \beta_tand\bar{\alpha}_t = \prod_{i=1}^t \alpha_i, the recursion can be written as
\begin{aligned} \mathbf{x}_t &= \sqrt{\alpha_t}\mathbf{x}_{t-1} + \sqrt{1 - \alpha_t}\boldsymbol{\epsilon}_{t-1} & \text{ ;where } \boldsymbol{\epsilon}_{t-1}, \boldsymbol{\epsilon}_{t-2}, \dots \sim \mathcal{N}(\mathbf{0}, \mathbf{I}) \\ &= \sqrt{\alpha_t \alpha_{t-1}} \mathbf{x}_{t-2} + \sqrt{1 - \alpha_t \alpha_{t-1}} \bar{\boldsymbol{\epsilon}}_{t-2} & \text{ ;where } \bar{\boldsymbol{\epsilon}}_{t-2} \text{ merges two Gaussians (*).} \\ &= \dots \\ &= \sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}\quad (2)\\ q(\mathbf{x}_t \vert \mathbf{x}_0) &= \mathcal{N}(\mathbf{x}_t; \sqrt{\bar{\alpha}_t} \mathbf{x}_0, (1 - \bar{\alpha}_t)\mathbf{I}) \end{aligned}
Usually, we can afford a larger update step when the sample gets noisier, so\beta_1 < \beta_2 < \dots < \beta_Tand therefore\bar{\alpha}_1 > \dots > \bar{\alpha}_T.
Reverse process (denoising): the denoising inference process of diffusion
The denoising process pθ is learned by optimizing the model parameters θ and is given by
p_\theta(\mathbf{x}_{t-1} \vert \mathbf{x}_t) = \mathcal{N}(\mathbf{x}_{t-1}; \boldsymbol{\mu}_\theta(\mathbf{x}_t, t), \boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t))\quad(3)
A U-Net is trained to predict xt-1 from xt according to (5), for any step t ∈ {1, ..., T }. The output of the U-Net is denoted as εθ, and the MSE loss used for training is
xt-1 is predicted from xt with
with
ε in each sampling step (5) is a stochastic element of DDPMS. In DDIMs, we set σt = 0, which results in a deterministic sampling process.
We can encode xt+1 given xt with
By applying (6) for t ∈ {0, ..., T - 1}, we can encode an image x0 to a noisy image xT. Then, we recover the identical x0 from xT by using (5) for t ∈ {T, ..., 1}.
Figure 4. The training and sampling algorithms in DDPM [3]
2. Methodology and Evaluation
2.1 Diffusion Deformable Model for 4D Temporal Medical Image Generation [11]
Motivations
In the field of medical imaging, temporal volume images with 3D+t (4D) information are often used to statistically analyze dynamic changes in anotomical structures and capture disease progression.
- Despite extensive development and advances in deep learning-based generative models for natural images, there exist limitations when it comes to approaches for temporal image generation such as 4D cardiac volume data;
- In contrast to CT and ultrasound, MRI requires a relatively long scan time to obtain the 4D images;
- Existing models based on GANs may introduce additional artefacts, which is unwanted to occur in the medical imaging area.
Method Overview
DDM (Diffusion Deformable Model) is composed of the diffusion module and the deformation module.
Figure 5. The overall framework of the proposed method.
Given the source image S, target T and the perturbed target xt:
1) The diffusion module learns deformation distribution between the source and target volumes and estimates the latent code c by using a score function of the DDPM;
2) c providing detailed spatial information of intermediate frames for 4D temporal volumes of the source image toward the target, is interpolated and fed into the deformation module;
3) The deformation module estimates the deformation fields φ according to the scaled c and generates deformed images S(φ) along the continuous deformation trajectory in the image registration manner (by warping the volume S with φ with the spatial transformation layer (STL)).
Experiments on 4D cardiac MRI data
trained and tested the proposed model DDM to generate 4D temporal cardiac MR images from the end-diastolic to the end-systolic phases for each subject
| Dataset | Characteristics |
|---|---|
ACDC |
|
Comparing methods: learning-based registration models
| Model | Descriptions | Parameters | |
|---|---|---|---|
| VM [39] | providing the intermediate frames between the source and target by scaling the estimated deformation fields φ, i.e. γ · φ | the weight of smooth regularization: 1 |
|
| VM-diff [40] | VM-diff with diffeomorphic constraint can generate the deformed images by integrating the velocity field with the timescales, i.e. . |
| |
Parameters settings:
| the noise level | from 10-6 to 10-2 |
| schedule u | 2000 |
| optimization algorithm | Adam |
| learning rate | 2 × 10-4 |
| λ (a hyper-parameter in the proposed loss function) | 20 |
| epochs | 800 |
| batch size | 1 |
Evaluation metrics:
| Indicator | Descriptions | Representation |
|---|---|---|
| PSNR (peak signal-to-noise ratio) |
| to quantify the image quality |
| NMSE (normalized mean square error) | ||
Dice score |
| to evaluate the accuracy of the diastolic-to-systolic deformation |
Results:
Using the source and target, the intermediate deformed images\textit{S}(\widetilde{\phi})(right) are generated using the deformation fields\widetilde{\phi}(left). References source: the ground-truth 4D images.
Figure 6. Visual comparison results of the temporal cardiac image generation
along the trajectory between the source and the target.
Observations:
- VM:\widetilde{\phi}only vary in scale without change in their relative spatial distributions.
→ the scaled movement of anatomical structures; - VM-diff: hardly deforms the source in the beginning, but sharply in the end;
- DDM:\widetilde{\phi}represent the dynamic changes depending on the positions.
→ The generated\textit{S}(\widetilde{\phi})have distinct changes from the source to the target.
Table 1. Quantitative evaluation results of the average values of PSNR, NMSE, Dice metrics and test runtime.
| Data | Method | PSNR (dB) ↑ | NMSE (×10-8) ↓ | Dice ↑ | Time (sec) ↓ |
|---|---|---|---|---|---|
Train | Initial DDM (Ours) | 29.683 (3.116) 32.788 (2.859) | 0.690 (0.622) 0.354 (0.422) | 0.700 (0.185) 0.830 (0.112) | - 0.456 |
Test | Initial VM VM-diff DDM (Ours) | 28.058 (2.205) 30.562 (2.649) ∗ 29.481 (2.473) ∗∗ 30.725 (2.579) | 0.790 (0.516) 0.490 (0.467) ∗ 0.602 (0.477) ∗∗ 0.466 (0.432) | 0.642 (0.188) 0.784 (0.116) ∗ 0.794 (0.104) 0.802 (0.109) | - 0.219 2.902 0.456 |
Standard deviations are shown in parentheses.
Asterisks: statistical difference of the baseline methods over DDM (∗∗: p < 0.005 and ∗: p < 0.05).
Figure 7. Boxplots of quantitative evaluation results on test data.
(LV-BP: left blood pool, LV-Myo: myocardium, LV: epicardium of the left ventricle, RV: right ventricle, LV+RV: the total cardiac region.)
Observations:
- PSNR: DDM shows slightly higher PSNR over VM and VM-diff;
- NMSE: DDM shows slightly lower NMSE and significantly lower NMSE than VM and VM-diff, respectively;
- Dice score: DDM shows slightly higher accuracy on Dice score over VM and VM-diff, achieving 80.2% with about 1% gain over the baseline methods;
- test runtime: DDM takes 0.456 seconds, significantly shorter than VM-diff (2.902 seconds), acceptably longer than VM (0.219 seconds);
- DDM: Test result on training data shows similar gains on all metrics when compared to that on test data.
Method sensitivity to changes of hyperparameter:
Analysis of the effect of the designed loss function according to DDM with various λ values:
Figure 8. Quantitative results over various λ values
Observations:
- When λ ↑, PSNR ↑ and NMSE ↓ initially, and both converge when it exceeds a certain level (λ = 5).
→ The large value of Ldeform does not affect the generation performance more; - When λ ↑, Dice score ↑ continuously.
→ Ldeform affects the registration accuracy, helping the diffusion module to estimate c to generate\textit{S}(\widetilde{\phi}); - When the model was trained only using the Ldeform: PSNR: 30.72, NMSE: 0.473×10-8, Dice scores: 0.799, worse than the optimal results of the proposed method.
→ The Ldiffuse is effective to learn the c for temporal images generation.
Conclusion:
Experimental results on 4D cardiac MRI data show that DDM achieves higher performance on the generation of temporal continuous deformed volumes from the end-diastolic to the systolic phase, outperforming the existing deformation methods which adjust the registration fields. It can provide distinct intermediate frames along the continuous trajectory between two real-time images in many medical scenarios such as analyzing dynamic changes in anatomical structures. This verifies the potential of DDM as a promising tool in realistic clinical applications.
2.2 Diffusion Models for Medical Anomaly Detection [12]
In this paper, a novel weakly supervised pixel-wise anomaly detection method based on DDIMs (denoising diffusion implicit models) is presented.
Motivations
- Current anomaly detection methods mainly relying on GANs [22,23,24] or autoencoder models [25,26] are often complicated to train or have difficulties in preserving fine details in the image;
- Training of GANs is challenging and requires a heavy work during hyperparameter tuning;
- Weakly supervised anomaly detection has aroused great interest in research and medical applications, as only image-level annotations are required for training;
Method Overview
DDIMs (Denoising Diffusion Implicit Models)
Figure 9. Combining the deterministic iterative DDIM noising and denoising schemes
with classifier guidance for image-to-image translation between input and output.
Figure 10. Workflow of the method
For the training: two unpaired sets of images respectively from healthy and diseased subjects. Only the image and the corresponding image-level label (healthy, diseased) are provided during training.
1) Iterative noising process: encoding the anatomical information of an image with the reversed sampling scheme of DDIMs.
2) Denoising process: using the deterministic sampling scheme in DDIM with classifier guidance to generate an image of a healthy subject.
3) The pixel-wise anomaly map is defined as the difference between the input diseased image and the synthetic output healthy image.
Results:
Figure 11. Results for two X-ray images of the CheXpert dataset for L = 500 and s = 100.
Observations:
- Our method: generates high quality images and preserves many details of the input image → detailed anomaly maps;
- The others: either cannot find the anomaly, or change details of the image.
Figure 12. Results for an image of the BRATS2020 dataset for L = 500 and s = 100.
Observations:
- DDIM (ours): Details of the input image can be mainly reconstructed;
- DDPM: The anatomical structure of input changes with the DDPM sampling scheme;
- Only the VAE tries to reconstruct the right ventricle.
Method sensitivity to changes of hyperparameter:
Hyperparameters: chosen for the DDPM as described in the appendix of [6]
| s | the classifier gradient scale |
| L | the noise level |
Figure 13. Average Dice and AUROC scores on the test set w.r.t. s for different L.
Horizontal bars: The scores for FP-GAN and VAE.
Figure 14. FLAIR image. The sampled results of various s for a fixed L = 500.
Figure 15. FLAIR image. The sampled results of various L for a fixed s = 100.
| Metrics | Descriptions | Calculation |
|---|---|---|
|
| calculated with the pixel-wise ground truth labels in BRATS2020 dataset |
| AUROC | the area under the receiver operating statistics |
Observations:
- s too small: The tumor cannot be removed;
- s too large: Additional artificial features mainly at the border of the brain are introduced. → Dice score↓
- L too small: The model lacks enough freedom to remove the tumor;
- L too large: Images are destructed.
Translation of a healthy subject:
Expected result: our method makes no change to the healthy image.
Figure 16. Results of the proposed method on a slice without tumor of the BRATS dataset.
Observations:
The final anomaly map is almost invisible.
→ There is almost no difference between input and the synthetic image.
→ The reconstruction preserves almost all details.
Conclusion:
The proposed method achieved excellent performance to accomplish high quality anomaly maps generation on two different medical datasets, through a detail-consistent translation from diseased image toward image without pathologies. The anomaly maps preserves many details of the original to-be-discusssed patient image as such translation only performs changes in the anomalous regions of it.
2.3 Fast Unsupervised Brain Anomaly Detection and Segmentation with Diffusion Models [13]
In this paper a method based on DDPMs to detect and segment brain anomalies is proposed.
Motivations
The solution of anomaly segmentation in medical imaging is of significance across many clinical tasks.
- Recent models for unsupervised anomaly detection in medical imaging such as transformers have some intrinsic limitations due to their autoregressive nature: extra images modeling requirement, the accumulation of prediction errors, and the inference times associated with data dimensionality and accordingly needed number of transformers;
- Non-autoregressive generative models - DDPMs have faster inference times compared to transformers;
- Deep generative models dispense with the necessity for either expensive manual labelling or images with anomalies in the training set [14,32,33,16], beneficial to anomaly detection and medical annotators.
Method Overview
1) VQ-VAE: to compress the input image;
2) Diffusion model: to model the latent space of the input image, where anomalous areas are identified.
By training the model on healthy data and then exploring its forward and reverse steps across its Markov chain, we can identify anomalous areas in the latent space and hence identify anomalies in the pixel space.
Experiments on brain data with synthetic and real lesions
| Dataset | Descriptions |
|---|---|
|
|
2. Anomaly Segmentation on MRI data
| Dataset | Descriptions | Usage |
|---|---|---|
| UKB [34] (UK Biobank) | 15,000 participants with the lowest lesion volume | Training set |
| UKB | white matter hyperintensities | Test set: FLAIR images |
| MSLUB [36] (Multiple Sclerosis dataset from the University Hospital of Ljubljana) | demyelinating lesions | |
| BRATS [19] (Multimodal Brain Tumor Image Segmentation Benchmark) | tumours | |
| WMH [35] (White Matter Hyperintensities Segmentation Challenge) | small vessel disease |
3. Inference Time of Anomaly Segmentation on CT data
This experiment focused on the inference time of anomaly segmentation methods in the analysis of intracerebral haemorrhages (ICH).
| Dataset | Descriptions |
|---|---|
| CROMIS [37] | Training set: 2D CT axial slices without ICH from 200 participants |
| CROMIS | Test set: 21 participants |
| KCH | |
| CHRONIC [38] |
Parameters settings:
| downsampling factor | f =4, f = 8 |
| DDIM L' | 400:600 (with 50 values evenly spaced) |
| reverse process steps | DDPM: 500, DDIM: 50 |
Table 4. Performance on anomaly segmentation using real 2D CT lesion data,
measured with the theoretically best possible DICE-score (\left \lceil\textit{DICE} \right \rceil).
| CROMIS | KCH | CHRONIC | Time [s] | ||
|---|---|---|---|---|---|
VAE (Dense) [14] | 0.185 0.146 0.286 0.220 | 0.353 0.292 0.483 0.469 | 0.171 0.099 0.285 0.210 | <1 <1 12 46 | <1min |
| DDPM (f = 8) (c) [Ours] DDPM (f = 4) (c) [Ours] Transformer [16] | 0.284 0.215 0.205 | 0.473 0.471 0.395 | 0.297 0.221 0.253 | 81 324 589 | 1min~10min |
| Ensemble [16] Transformer (f = 4) [Ours] Ensemble (f = 4) [Ours] | 0.241 0.356 0.471 | 0.435 0.482 0.631 | 0.268 0.116 0.122 | 4907 8047 >8000 |
|
Added step (d) of our method: using a DDIM to perform the reverse process.
Observations:
- Our method using the DDIM sampler had a greatly improved inference time under 1 minute while keeping a similar performance;
- The transformer-based methods: slower than all our methods;
- Inference times increase as the length of the input sequence grows (changing from f = 8 to f = 4).
Conclusion:
In addition to the image quality, fast inference time is a crucial factor for application in time-critical medical scenarios. The results of a series of experiments on both synthetic and real lesions data demonstrated the faster inference time property of the proposed methods compared to autoregressive transformer-based approaches. Also, it outperformd the single tranformer in most cases (in some cases, worse quality than the ensemble of transformers). These makes their clinical application feasible.
3. Comparison
The DDM method in "Diffusion Deformable Model for 4D Temporal Medical Image Generatio" has the ability to perserve topology features of the input source image while analysing the anotomical changes. It is not only better in image quality, but also faster in generation efficiency, which is significant for real-time imaging. Similarly in anomaly detection, the DDIM-based method in "Diffusion Models for Medical Anomaly Detection" is also able to mainly reconstruct the original details of the regions without pathologies in the source image when generating anomaly maps. It is weakly supervised with simpler training process and without expensive manual labeling, straightforward to fit different datasets. However, it can be time-consuming in some cases where the iterative image generation process leads to a longish computation time of a complete image translation, which can be speeded up but with degradation of the image quality. The DDPM-based method in "Fast Unsupervised Brain Anomaly Detection and Segmentation with Diffusion Models" has also a fast inference time, superior in scenarios where there is time constraint (especially when using DDIMs). Besides, it has the ability of elimination of the unidirectional bias and avoidance of accumulated prediction errors during the process removing anomalies from the input image. Nevertheless, in some cases it cannot achieve the same-level quality image in anomaly detection and segmentation as an ensemble of transformers do.
4. Review
In the field of medical imaging, many clinical tasks such as analysing changes of anotomical structures, anomaly detection and segmentation used to be low-efficient because of the manual operation and needs for expertise. The development and introduction of deep learning-based methods greatly improve the efficiency of diagnosis and treatment, and liberate the hands of doctors to allocate more energy on prognosis and treatment plan making. Nowadays, generative model based methods have benefited pathologies detection a lot as a great assistant. Autoregressive transformer-based approaches also contribute much to lesions segmentation. But people can never stop moving forward, just as people still keep working with the aforementioned methods when they already have the technology of CT x-ray, MRI, ultrasound and so on in the near past. The diffusion model is one of the current trends, interestingly inspired by a physical thermodynamic phenomenon. People are amazed of how the first people finished such creation but it did work after trials just as many model proposed in deep learning area. The mathematical framework of diffusion model has already been completed years before today's popularity of if, which started with the proposed DDPM in 2020. Most of the diffusion models currently employed are derived from DDPM and it led to the later trend. It can be seen that the birth and popularity of a model often requires time and opportunity. DDPMs have caught the attention of the medical imaging community, as they surpass currently popular methods based on GANs, VAE and autoregressive models to achieve a higher quality and efficiency in image processing and analysis. It is much likely that diffusion models have the potential to be further improved and extended, bringing more advances to medical imaging.
5. Reference
[1] Aditya Ramesh et al. “Hierarchical Text-Conditional Image Generation with CLIP Latents." arxiv Preprint arxiv:2204.06125 (2022).
[2] Chitwan Saharia & William Chan, et al. “Photorealistic Text-to-Image Diffusion Models with Deep Language Understanding." arxiv Preprint arxiv:2205.11487 (2022).
[3] Jonathan Ho et al. “Denoising Diffusion Probabilistic Models.” arxiv Preprint arxiv:2006.11239 (2020). [code]
[4] Jascha Sohl-Dickstein et al. “Deep Unsupervised Learning using Nonequilibrium Thermodynamics.” ICML 2015.
[5] https://www.sciencefacts.net/diffusion.html
[6] Dhariwal, P., Nichol, A.: Diffusion models beat gans on image synthesis. Advances in Neural Information Processing Systems 34 (2021)
[7] Sasaki, H., Willcocks, C.G., Breckon, T.P.: Unit-ddpm: Unpaired image translation with denoising diffusion probabilistic models. arXiv preprint arXiv:2104.05358 (2021)
[8] Baranchuk, D., Voynov, A., Rubachev, I., Khrulkov, V., Babenko, A.: Labelefficient semantic segmentation with diffusion models. In: International Conference on Learning Representations (2022)
[9] Saharia, C., Chan, W., Chang, H., Lee, C.A., Ho, J., Salimans, T., Fleet, D.J., Norouzi, M.: Palette: Image-to-image diffusion models. arXiv preprint arXiv:2111.05826 (2021)
[10] Kim, B., Han, I., Ye, J.C.: Diffusemorph: Unsupervised deformable image registration along continuous trajectory using diffusion models. arXiv preprint arXiv:2112.05149 (2021)
[11] B. Kim and J. Ye, “Diffusion Deformable Model for 4D Temporal Medical Image Generation.” Accessed: Jan. 28, 2023. [Online]. Available: https://arxiv.org/pdf/2206.13295.pdf
[12] J. Wolleb, F. Bieder, R. Sandkühler, and P. C. Cattin, “Diffusion Models for Medical Anomaly Detection,” arXiv.org, 2022, doi: 10.48550/arXiv.2203.04306.
[13] Walter et al., “Fast Unsupervised Brain Anomaly Detection and Segmentation with Diffusion Models,” arXiv.org, 2022, doi: 10.48550/arXiv.2206.03461.
[14] Baur, C., Denner, S., Wiestler, B., Navab, N., Albarqouni, S.: Autoencoders for unsupervised anomaly segmentation in brain MR images: a comparative study. Medical Image Analysis 69, 101952 (2021)
[15] Schlegl, T., Seeböck, P., Waldstein, S.M., Langs, G., Schmidt-Erfurth, U.: f-anogan: Fast unsupervised anomaly detection with generative adversarial networks. Medical image analysis 54, 30–44 (2019)
[16] Pinaya, W.H.L., Tudosiu, P.D., Gray, R., Rees, G., Nachev, P., Ourselin, S., Cardoso, M.J.: Unsupervised brain anomaly detection and segmentation with transformers. arXiv preprint arXiv:2102.11650 (2021)
[17] Menze, B.H., Jakab, A., Bauer, S., Kalpathy-Cramer, J., Farahani, K., Kirby, J., Burren, Y., Porz, N., Slotboom, J., Wiest, R., et al.: The multimodal brain tumor image segmentation benchmark (BRATS). IEEE transactions on medical imaging 34(10), 1993–2024 (2014)
[18] Bakas, S., Akbari, H., Sotiras, A., Bilello, M., Rozycki, M., Kirby, J.S., Freymann, J.B., Farahani, K., Davatzikos, C.: Advancing the cancer genome atlas glioma MRI collections with expert segmentation labels and radiomic features. Scientific data 4(1), 1–13 (2017)
[19] Bakas, S., Reyes, M., Jakab, A., Bauer, S., Rempfler, M., Crimi, A., Shinohara, R.T., Berger, C., Ha, S.M., Rozycki, M., et al.: Identifying the best machine learning algorithms for brain tumor segmentation, progression assessment, and overall survival prediction in the BRATS challenge. arXiv preprint arXiv:1811.02629 (2018)
[20] Irvin, J., Rajpurkar, P., Ko, M., Yu, Y., Ciurea-Ilcus, S., Chute, C., Marklund, H., Haghgoo, B., Ball, R., Shpanskaya, K., et al.: Chexpert: A large chest radiograph dataset with uncertainty labels and expert comparison. In: Proceedings of the AAAI conference on artificial intelligence. vol. 33, pp. 590–597 (2019)
[21] Goodfellow, I., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., Courville, A., Bengio, Y.: Generative adversarial nets. Advances in neural information processing systems 27 (2014)
[22] Siddiquee, M.M.R., Zhou, Z., Tajbakhsh, N., Feng, R., Gotway, M.B., Bengio, Y., Liang, J.: Learning fixed points in generative adversarial networks: From image-to-image translation to disease detection and localization. In: Proceedings of the IEEE/CVF international conference on computer vision. pp. 191–200 (2019)
[23] Baumgartner, C.F., Koch, L.M., Tezcan, K.C., Ang, J.X., Konukoglu, E.: Visual feature attribution using wasserstein gans. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. pp. 8309–8319 (2018)
[24] Wolleb, J., Sandkühler, R., Cattin, P.C.: Descargan: Disease-specific anomaly detection with weak supervision. In: International Conference on Medical Image Computing and Computer-Assisted Intervention. pp. 14–24. Springer (2020)
[25] Zhou, C., Paffenroth, R.C.: Anomaly detection with robust deep autoencoders. In: Proceedings of the 23rd ACM SIGKDD international conference on knowledge discovery and data mining. pp. 665–674 (2017)
[26] Kingma, D.P., Welling, M.: An introduction to variational autoencoders. arXiv preprint arXiv:1906.02691 (2019)
[27] Zimmerer, D., Kohl, S.A., Petersen, J., Isensee, F., Maier-Hein, K.H.: Contextencoding variational autoencoder for unsupervised anomaly detection. arXiv preprint arXiv:1812.05941 (2018)
[28] Chen, X., Konukoglu, E.: Unsupervised detection of lesions in brain mri using constrained adversarial auto-encoders. arXiv preprint arXiv:1806.04972 (2018)
[29] Marimont, S.N., Tarroni, G.: Anomaly detection through latent space restoration using vector quantized variational autoencoders. In: 2021 IEEE 18th International Symposium on Biomedical Imaging (ISBI). pp. 1764–1767. IEEE (2021)
[30] Nichol, A.Q., Dhariwal, P.: Improved denoising diffusion probabilistic models. In: Proceedings of the 38th International Conference on Machine Learning. vol. 139, pp. 8162–8171. PMLR (2021)
[31] Otsu, N.: A threshold selection method from gray-level histograms. IEEE transactions on systems, man, and cybernetics 9(1), 62–66 (1979)
[32] You, S., Tezcan, K.C., Chen, X., Konukoglu, E.: Unsupervised lesion detection via image restoration with a normative prior. In: International Conference on Medical Imaging with Deep Learning. pp. 540–556. PMLR (2019)
[33] Pawlowski, N., Lee, M.C., Rajchl, M., McDonagh, S., Ferrante, E., Kamnitsas, K., Cooke, S., Stevenson, S., Khetani, A., Newman, T., et al.: Unsupervised lesion detection in brain ct using bayesian convolutional autoencoders (2018)
[34] Sudlow, C., Gallacher, J., Allen, N., Beral, V., Burton, P., Danesh, J., Downey, P., Elliott, P., Green, J., Landray, M., et al.: Uk biobank: an open access resource for identifying the causes of a wide range of complex diseases of middle and old age. PLoS medicine 12(3), e1001779 (2015)
[35] Kuijf, H.J., Biesbroek, J.M., De Bresser, J., Heinen, R., Andermatt, S., Bento, M., Berseth, M., Belyaev, M., Cardoso, M.J., Casamitjana, A., et al.: Standardized assessment of automatic segmentation of white matter hyperintensities and results of the wmh segmentation challenge. IEEE transactions on medical imaging 38(11), 2556–2568 (2019)
[36] Lesjak, Ž., Galimzianova, A., Koren, A., Lukin, M., Pernuš, F., Likar, B., Špiclin, Ž.: A novel public mr image dataset of multiple sclerosis patients with lesion segmentations based on multi-rater consensus. Neuroinformatics 16(1), 51–63 (2018)
[37] Wilson, D., Ambler, G., Shakeshaft, C., Brown, M.M., Charidimou, A., Salman, R.A.S., Lip, G.Y., Cohen, H., Banerjee, G., Houlden, H., et al.: Cerebral microbleeds and intracranial haemorrhage risk in patients anticoagulated for atrial fibrillation after acute ischaemic stroke or transient ischaemic attack (cromis-2): a multicentre observational cohort study. The Lancet Neurology 17(6), 539–547 (2018)
[38] Mah, Y.H., Nachev, P., MacKinnon, A.D.: Quantifying the impact of chronic ischemic injury on clinical outcomes in acute stroke with machine learning. Frontiers in neurology 11, 15 (2020)
[39] Balakrishnan, G., Zhao, A., Sabuncu, M.R., Guttag, J., Dalca, A.V.: An unsupervised learning model for deformable medical image registration. In: Proceedings of the IEEE conference on computer vision and pattern recognition. pp. 9252–9260 (2018)
[40] Dalca, A.V., Balakrishnan, G., Guttag, J., Sabuncu, M.R.: Unsupervised learning for fast probabilistic diffeomorphic registration. In: International Conference on Medical Image Computing and Computer-Assisted Intervention. pp. 729–738. Springer (2018)