This blog post summarizes the paper "TransMorph: Transformers for Medical Image Registration". The paper's authors are Junyu Chen, Eric C. Frey, Yufan He, William P. Segars, Ye Li, Yong Du.
Author: Idil Ünlü
1. Introduction
1.1 Problem Statement : Image Registration
Image registration is aligning or superimposing two or more images of the same scene or object. The goal of image registration is to correct misalignment or distortion between images that may result from motion, changes in viewing angle, or different sensor characteristics. It is the task of finding a mapping between to warp or deform one image to match the other. This mapping is also known as the deformation field. It is typically a continuous, one-to-one function. Once the deformation field is calculated, images can be registered and combined to provide a more accurate and detailed representation of the scene or object.
In the medical domain, image registration is used to align and combine images from different modalities, such as CT, MRI, and PET scans, or to align images acquired at different times, such as before and after treatment. This allows doctors and researchers to diagnose and monitor diseases more accurately, plan and evaluate treatments, and conduct research.
Image registration can be challenging due to image artifacts and variations in patient anatomy and imaging conditions. Problems include dealing with variations in image intensity, noise, deformations, and the lack of clear anatomic features in some images. These challenges are particularly pronounced when registering images from different modalities, such as X-ray, CT, MRI, and ultrasound. Each modality has its own intrinsic properties, such as contrast, resolution, and field of view, which can make registration difficult.
1.1.2 Diffeomorphic Image Registration
In the scope of medical applications, unless we consider the case that the patient underwent surgery, we expect the body parts being imaged to be continuous. Therefore the deformation field used in the registration process should be smooth and invertible.
However, some methods, especially Deep Neural Network based methods, may produce non-smooth deformation fields. To address this issue, a regularization term as in Eq.1 can be introduced to enforce spatial smoothness in the deformation field. Also, to ensure topology preservation and invertibility, diffeomorphic transformations are used. They utilize time-varying velocity fields and deform the images in a way that does not introduce any gaps, discontinuities, or singularities.
2. Methods
In recent years, researchers have been using deep learning-based methods to address these problems. They have been shown to improve the registration accuracy, robustness, and computational efficiency of image registration algorithms.
Before the advent of deep learning and neural networks, the most common approach was optimization-based registration.
2.1 Traditional Methods
Optimization-based registration methods involve defining a similarity metric to measure the difference between the source and target images and then using optimization algorithms to find the optimal transformation that aligns the source image with the target image.
One of the most widely used optimization-based registration methods is the Demons algorithm. This method uses a differential equation to describe the image deformation and an iterative optimization algorithm to find the optimal solution. The Demons algorithm starts with an initial transformation and iteratively updates the transformation to minimize the difference between the source and target images.
Figure 1: Conventional paradigm of the image registration [1]
Equation 1: Energy function of the image registration [1]
Another popular optimization-based registration method is B-spline registration. This method uses a B-spline grid to represent the image deformation, and an optimization algorithm to find the optimal B-spline coefficients that align the source image with the target image.
Even though both demons and B-spline registration were excessively used in medical image registration, they have certain limitations. They can be sensitive to the choice of similarity metric and optimization algorithm, and can be computationally expensive, particularly for large images or for registration of images with large deformations.
2.2 Deep-Learning Based Methods
Recently, deep learning-based registration methods such as CNNs, U-Nets, and autoencoders have been introduced to overcome the limitations of traditional optimization-based registration methods. These methods use neural networks to learn the complex relationships between images and can handle large deformations and variability in image intensity.
Convolutional networks have limitations in modeling explicit long-range spatial relations due to the intrinsic locality of the kernel operations. To address this, the U-Net architecture was introduced, which includes down-sampling and up-sampling operations to increase the receptive field theoretically. However, in practice, the effective receptive field is still much smaller than expected, and the network's ability to perceive semantic information and model long-range relationships is limited.
Several works have been proposed to address this limitation, such as the nested U-Net (U-Net++), dilated convolution, recurrent convolutional operations, and ResUNet++, which incorporates attention mechanisms. Although these showed promising performance in other medical imaging fields, more work needs to be done on using advanced network architectures for medical image registration.
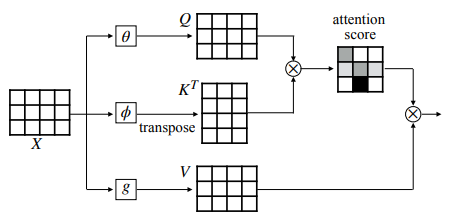
On the other hand, Transformers, a deep learning model initially developed for natural language processing tasks, has been shown to have potential applications in computer vision tasks. It uses self-attention mechanisms to identify the essential parts of an input sequence (such as an image). Thus, its ability to capture long-range spatial information is superior to traditional convolutional neural networks. The superiority of Transformers comes from the use of self-attention mechanism steps which are as follows:
- The input is transformed into a set of queries, keys, and values in the first stage.
- Queries and keys are used to compute the set of attention scores which is a measure of the importance of each part of the input to another.
- Values are weighted according to attention scores to get a new input representation. Then, this new representation can be used as input to the successive layers.
Figure 2: Scheme of self-attention mechanism and QKV model
The self-attention mechanism enables the model to attend to different parts of the input at different times based on the attention scores. So, it allows the model to capture the complex relationship between different parts of the input and incorporate this connection in the further steps as well.
The success of Transformers has led to the development of Vision Transformer (ViT), a purely self-attention-based network that achieved state-of-the-art results in image recognition.
Figure 3: A model overview of Vision Transformers [2]
Subsequently, Swin Transformers have demonstrated superior performance in object detection and semantic segmentation. So, recently, Transformer-related methods have gained attention in medical imaging, particularly for the task of image segmentation. Unlike traditional transformer architectures that process data as a sequence, Swin Transformer processes the input data as a set of windows or patches, each processed independently and in parallel by the self-attention mechanism. By processing the input data in a more local and parallel manner, the SWIN Transformer can be more computationally efficient and scalable to larger image sizes than traditional Transformer architectures.
Following Swin Transformer, a hybrid Transformer-ConvNet framework called TransMorph is proposed for volumetric medical image registration[1]. The framework employs the Swin Transformer as an encoder to capture the spatial correspondence between the input moving and fixed images, and a ConvNet decoder processes the information provided by the Transformer encoder into a dense displacement field.
2.3 TransMorph Architecture
Figure 4: Overview of TransMorph Architecture [1]
As shown in Fig. 4, the network starts by dividing the input into non-overlapping 3D patches. Then, each patch is flattened and considered as a "token" to be processed by a linear projection block.
The problem here is that the linear projection operates on flattened image patches and does not utilize the location of those tokens for further steps. To make use of tokens' relative location, Transformer-based models often add positional embeddings to these operations. If positional embeddings are not employed, there might be a loss of information in the network.
However, image registration is a pixel-level task, and the decoder's task includes generating an output image having the exact dimensions/resolution as the input image. Then, spatial mismatches between the input and output images are calculated to form a loss function that would be backpropagated into the encoder network. In other words, Transformers inherently includes the token's positional information which will be further discussed in Results section.
After the linear projection layers, there are several consecutive Swin Transformer and patch merging blocks. Following that, the decoder consists of consecutive upsampling and convolution blocks. Feature maps extracted from Swin Transformers are first upsampled and then concatenated with the feature map from skip connections before getting into convolutional layers [4].
Figure 5: Simplified diagram of TransMorph [1]
3. Results
The performance of TransMorph is compared to 12 different other architectures as follows:
- Non-deep-learning Based Methods
- SyN [5] (symmetric image normalization)
- NiftyReg [6]
- deedsBCV [7]
- LDDMM [8]
- Deep-learning Based Methods
- VoxelMorph [9]
- VoxelMorph-diff [10]
- CycleMorph [11]
- MIDIR [12]
- Transformer-based Methods
- ViT-V-Net [13]
- PVT [14]
- CoTr [15]
- nnFormer [16]
Also, variants of the TransMorph with additional constraints or varying hyperparameters are tested. Apart from those, an ablation study is conducted to see which building blocks in TransMorph have a crucial effect on the final results. Results are validated with three different datasets and one public dataset for the registration challenge. Since the Dice score is widely used in the image registration domain [17], the success of the results will be primarily evaluated according to Dice scores in the following sections.
Figure 6: Validation Dice scores for inter-patient brain MRI registration [1]
As shown in Fig.6, TransMorph achieved > 0.7 dice scores earlier than 20 epochs, which indicates that it is faster in learning the spatial correspondences compared to the other models. Besides, it performed better than other Transformer-based models having a similar number of parameters and complexity. We can deduce that the Swin Transformer architecture is more effective than other Transformer models.
Another indicator of the performance in deep learning models is the shape of the training curve. It consists of two phases; transient and minimization. A shorter transient phase means the algorithm converges faster, which in return saves time, computing resources, and costs. As seen in the graph on the right side, TransMorph variants have shorter transient phases than that of VoxelMorph, which is CNN-based.
Overall, Transformer-based models outperformed ConvNet-based models in terms of dice score and convergence speed as also shown in Table 1.
Table 1: Quantitative evaluation of the inter-patient and the atlas-to-patient brain MRI registration [1]
Apart from the dice score, the percentage of non-positive values in the determinant of the Jacobian matrix on the deformation field is used (|Jφ | ≤ 0) for performance metrics. The determinant of the Jacobian of the deformation field is the measure of stretching or compression that occurs during the deformation. If it is positive, it means that the object's volume is preserved during the deformation, and the object is undergoing an "invertible" deformation, which was one of the conditions of Deformable Image Registration(DIR) mentioned in section 1.1.2. On the other hand, a negative determinant of the Jacobian matrix indicates that the object is undergoing a "non-invertible" deformation which is not desired in the DIR case. TransMorph again outperforms unless the model being compared is specifically implemented with diffeomorphic constraints.
Figure 7: Quantitative evaluation results of the ablation studies on three different datasets[1]
Since the TransMorph block is relatively big, ablation studies are conducted to see whether everything is necessary or not. Violin plots in Fig. 7 show that eliminating skip connections in Transformer blocks results in a drop in dic score, the most drastically in Atlas-to-patient Brain MRI registration case, from 0.753 to 0.740. The results from all three datasets confirm that using skip connections in Transformers improves the performance. On the other hand, removing skip connections in convolutional layers has a minor effect.
Similarly, positional embeddings almost perform as same as the case tokens are shuffled. In the "w/shuffling" case, positional embeddings are not used; instead, the tokens' position is randomly shuffled. Scores in Table 2 show that positional embedding brings no additional improvement but extra parameters. It could be skipped to decrease computational complexity.
Table 2: Comparison of Dice scores on the test dataset for ablation study [1]
Another measure of success is the effective receptive field(ERF) [18]. In theory, the receptive field of CNN-based models is the entire image if the network is deep enough. However, the theoretical receptive field doesn't focus on the pixels' contribution to displacement fields as much as ERF. As shown in Fig. 8, TransMorph's ERF substantially increases. It once more verifies that TransMorph outperformed VoxelMorph in terms of taking spatial relationships into account.
Figure 8: Effective receptive field (ERF) of VovelMorph vs TransMorph[1]
4. Personal Review
Strengths
When I read this paper, I first asked myself how or why they came up with the idea of combining Transformers with Convolutional Networks. Transformers being the state-of-art, both architectures proved their success in image processing tasks. However, merging these two was a new contribution and they show their reasonings step by step along the paper.
For example, feature maps generated from transformers are generally abstract, and they don't contain any human-readable information. In contrast, convolutional layers provide high-resolution and meaningful feature maps, as shown in Fig. 9. So, introducing ConvNets and skip connections instead of using a Transformers-only model makes progress trackable and prevents loss of information. As in this case, they always support their arguments with strong visuals.
Figure 9: Examples of feature maps in TransMorph's skip connections
( Middle panel: Feautre maps in skip connections from the top two convolutional layers in Figure 4 denoted with green arrows. Right panel: Feature maps in the skip connections of the Swin Transformer blocks )
Overall:
- They verify their assumptions both qualitatively and quantitatively in a very understandable way
- They haven't only used private datasets but also public datasets used for the image registration challenge
Weaknesses
As opposed to papers introducing a new model architecture, they don't provide grid search results for hyperparameter choice or don't try out different loss functions but use the ones that are proposed by previous papers.
Apart from that, as shown in Fig. 10 and 11, the advantages of TransMorph architecture come with their costs. Its complexity is more than double of CNN-based VoxelMorph, and the total number of parameters is drastically different. Even though the transient phase of TransMorph is shorter, as in Fig. 6, it is disputable that it can decrease the computation time and costs by itself with that many parameters.
So my question is: Are improvements worth the parameter overhead and additional computational complexity?
Figure 10: Computational complexity comparisons between deep-learning based registration [1]
Figure 11: The number of parameters in deep-learning-based models [1]
5. Presentation
6. References
[1] J. Chen, E. C. Frey, Y. He, W. P. Segars, Y. Li, and Y. Du, “TransMorph: Transformer for unsupervised medical image registration,” Medical Image Analysis, vol. 82, p. 102615, Nov. 2022, doi: 10.1016/j.media.2022.102615
[2] J. Chen, Y. He, E. C. Frey, Y. Li, and Y. Du, “ViT-V-Net: Vision Transformer for Unsupervised Volumetric Medical Image Registration.” arXiv, Apr. 13, 2021. Accessed: Feb. 02, 2023. [Online]. Available: http://arxiv.org/abs/2104.06468
[3] A. Sotiras, C. Davatzikos, and N. Paragios, “Deformable Medical Image Registration: A Survey,” IEEE Trans. Med. Imaging, vol. 32, no. 7, pp. 1153–1190, Jul. 2013, doi: 10.1109/TMI.2013.2265603.
[4] M. Raghu, T. Unterthiner, S. Kornblith, C. Zhang, and A. Dosovitskiy, “Do Vision Transformers See Like Convolutional Neural Networks?” arXiv, Mar. 03, 2022. Accessed: Feb. 02, 2023. [Online]. Available: http://arxiv.org/abs/2108.08810
[5] Avants, B.B., Epstein, C.L., Grossman, M., Gee, J.C., 2008. Symmetric diffeomorphic image registration with cross-correlation: evaluating automated labeling of elderly and neurodegenerative brain. Medical image analysis 12, 26–41.
[6] Modat, M., Ridgway, G.R., Taylor, Z.A., Lehmann, M., Barnes, J., Hawkes,D.J., Fox, N.C., Ourselin, S., 2010. Fast free-form deformation using graph-ics processing units. Computer methods and programs in biomedicine 98, 278–284.
[7] Heinrich, M.P., Maier, O., Handels, H., 2015. Multi-modal multi-atlas segmentation using discrete optimisation and self-similarities. VISCERAL Challenge@ ISBI 1390, 27
[8] Beg, M.F., Miller, M.I., Trouvé, A., Younes, L., 2005. Computing large deformation metric mappings via geodesic flows of diffeomorphisms. International journal of computer vision 61, 139–157.
[9] Balakrishnan, G., Zhao, A., Sabuncu, M.R., Guttag, J., Dalca, A.V., 2019. Voxelmorph: a learning framework for deformable medical image registration. IEEE transactions on medical imaging 38, 1788–1800.
[10] Dalca, A.V., Balakrishnan, G., Guttag, J., Sabuncu, M.R., 2019. Unsupervised learning of probabilistic diffeomorphic registration for images and surface. Medical image analysis 57, 226–236.
[11] Kim, B., Kim, D.H., Park, S.H., Kim, J., Lee, J.G., Ye, J.C., 2021. Cyclemorph: Cycle consistent unsupervised deformable image registration. Medical Image Analysis 71, 102036.
[12] Qiu, H., Qin, C., Schuh, A., Hammernik, K., Rueckert, D., 2021. Learning diffeomorphic and modality-invariant registration using b-splines, in: Medical maging with Deep Learning.
[13] Chen, J., He, Y., Frey, E.C., Li, Y., Du, Y., 2021a. Vit-v-net: Vision transformer for unsupervised volumetric medical image registration. arXiv preprint arXiv:2104.06468 .
[14] Wang, W., Xie, E., Li, X., Fan, D.P., Song, K., Liang, D., Lu, T., Luo, P., Shao, L., 2021c. Pyramid vision transformer: A versatile backbone for dense prediction without convolutions. arXiv preprint arXiv:2102.12122 .
[15] Xie, Y., Zhang, J., Shen, C., Xia, Y., 2021. Cotr: Efficiently bridging cnn and transformer for 3d medical image segmentation. arXiv preprint arXiv:2103.03024 .
[16] Zhou, H.Y., Guo, J., Zhang, Y., Yu, L., Wang, L., Yu, Y., 2021. nnformer:Interleaved transformer for volumetric segmentation. arXiv:2109.03201.
[17] Dice, L.R., 1945. Measures of the amount of ecologic association between species. Ecology 26, 297–302.
[18] Luo, W., Li, Y., Urtasun, R., Zemel, R., 2016. Understanding the effective receptive field in deep convolutional neural networks, in: Proceedings of the 30th International Conference on Neural Information Processing Systems, pp. 4905–4913.