Author: Leonhard Zirus 

Supervisor: Mohammad Farid Azampour 

1. Introduction / Motivation

In computer vision, optimal network performance depends on extensive datasets of clean, high-quality images. In medical imaging, obtaining such datasets is challenging due to the high cost and resource intensity of acquiring detailed CT or MRI scans, often compromised by noise and artifacts. Generative AI models have shown promise in producing high-quality synthetic images to supplement existing datasets, improving robustness and accuracy in computer vision networks [1,7].

However, large datasets and the computational intensity of training these models remain significant hurdles. The synthetic images often lack the intricate details necessary for accurate medical analysis. Thus, continuous advancements in generative AI models are essential. [13]

This blog post explores how integrating wavelet transformations can enhance diffusion models, potentially improving the fidelity and quality of generated images. By capturing frequency and spatial information, wavelet transformations can address persistent challenges in generating high-quality synthetic images, making computer vision training more efficient and effective. We will examine recent studies and methodologies and evaluate them in a medical context to understand how these advancements can benefit current research in medical imaging.

2. Background

To fully understand and evaluate the presented research, it is important to understand the underlying principles and methodologies. The following chapter briefly introduces the idea of generative models and explains the fundamentals of wavelet transforms. 

2.1. Generative Models

Generative models are one type of machine learning model designed to generate new data samples that resemble a given training dataset. These models learn the underlying distribution of the data and can then produce highly realistic and diverse new data samples similar to the original data. Some typical applications include generating images, text, and audio. The most common implementations also used in medical imaging are Variational Autoencoders (VAEs) and Generative Adversarial Networks (GANs). [11]

Score-Based Generative Models:

While traditional generative models learn to produce new samples directly, Score-Based Generative Models (SGMs) learn to estimate a score function of the data distribution. The score function represents the gradient of the log probability density, guiding the model to generate new samples by following these gradients. Two common SGM types are Denoising Score Matching (DSM) and Stochastic Differential Equations (SDE). [11]

Diffusion models:

Diffusion models have quickly become one of the more widely used techniques in data generation in recent years. They are deep generative models using two stages to generate new data. Starting with forward diffusion, in which the data is slowly altered over a series of steps by adding Gaussian noise. In the following reverse diffusion stage, the models learn to reverse these changes step by step to recover the original data. By learning to generate the original input from noise, the diffusion model develops the ability to produce new data similar to the original data distribution it trained on. While they are known for producing high-quality and varied results, they are often slow because they require many steps to generate new samples. [2]

By relying on estimating the gradient of the data distribution, known as the score function, to guide the reverse process, diffusion models are also a subset of SGMs.

2.2. Wavelet Transforms

Wavelet transforms are mathematical transforms similar to the well-known Fourier transform. They can decompose data into different frequency components while providing both time and frequency localization, unlike the Fourier transform, which loses the time information. This adaptability allows for efficient representation and analysis of signals with non-stationary properties, making wavelet transforms invaluable in various scientific fields, from signal processing over data compression to smoothing and image denoising, to name a few. [10]

When applied to images, wavelet transforms are used for multi-resolution analysis, enabling the examination of images at various levels of detail. This capability is crucial for tasks such as image compression, denoising, and feature extraction. For instance, in image compression, wavelet transforms can efficiently represent image data by focusing on areas with significant information and discarding redundant data, thus reducing file size while preserving quality [12]. Similarly, for image denoising, wavelet transforms isolate and remove noise while retaining essential features, improving overall image clarity [3]. These applications leverage the inherent properties of wavelets to handle the complex structures present in images, providing a robust toolset for image analysis and processing. 

Figure 1 serves as an example of how the application of a discrete wavelet transform (DWT) decomposes the image into multiple sub-bands:

• LL (Low-Low): Approximation of the original image, capturing the low-frequency components.
• LH (Low-High): Horizontal edge details; representing low-frequency in the horizontal direction and high-frequency in the vertical direction.
• HL (High-Low): Vertical edge details; representing high frequency in the horizontal direction and low frequency in the vertical direction.
• HH (High-High): High-frequency components; capturing the diagonal details and fine textures in the image

The transformation in this so-called wavelet domain allows for multi-resolution analysis and enhances various image-processing tasks.

Figure 1: Images' sub-bands after discrete wavelet transform of a previously smoothed image. Cropped from figure from [7]

3. Integrating Wavelet-Enhanced Generative Models

In the following sections, we will examine three distinct approaches that utilize wavelet transforms to enhance generative models for various applications. Each method presents a unique implementation, leveraging the strengths of wavelet transformations to improve the performance and quality of generative models in different contexts. By analyzing these methods, we aim to uncover their advantages and disadvantages and evaluate the potential for their use in the medical context.

3.1. Medical Imaging Advancements

The first method is introduced by Wu et al. in their paper "Wavelet-Improved Score-Based Generative Model for Medical Imaging" [13]. SGMs are widely used in medical imaging but require high-quality training datasets. Unfortunately, specifically, modalities like low-dose CT, sparse-view CT, and fast MRI often exhibit noise and artifacts, challenging SGMs (see Figure 2). They propose an adaptive wavelet sub-network used as an effective denoising mechanism, integrated into a unified, jointly trained framework with an SGM network.

Figure 2: (a) ground truth (b), (c) reconstruction result of SGM trained with clean and noisy images respectively (d), (e), (f) differences between reconstructed images and the ground truth respectively

3.1.1. Method

The unified framework combines a wavelet sub-network and an SGM sub-network in a joint learning approach, where each improves the other's results. The wavelet sub-network denoises training images, helping the SGM learn the scoring function more accurately and generate better reconstructions. These can, in turn, help to refine the wavelet sub-network. Figure 3 (a) illustrates this: training images are fed from the noisy dataset through the wavelet sub-network to the SGM. The improved reconstructed images are later fed back to the wavelet for refinement.

Langevin dynamics sampling can produce diverse results without guidance or regularization during reconstruction. To address this, wavelet total variation regularization is applied to guide the sampling process, ensuring data consistency between the reconstructed image and the measurement data. This approach improves the reconstruction quality through regularization, demonstrated in CT and MRI reconstruction tasks. The process involves iterative updates that refine the reconstructed images, as illustrated in Figure 3 (b). For additional details and mathematical explanation, please refer to the original paper.

Figure 3: showing unified framework illustrated. (a) training phase, same for CT and MRI (b) regularization integrated in the reconstruction process, top for CT, bottom for MRI

3.1.2. Experiments and Results

Extensive experimentation was conducted to validate the proposed methods, focusing on low-dose CT, sparse-view CT, and MRI reconstruction. Reconstruction quality was assessed using the Peak Signal-to-Noise Ratio (PSNR) and Structural Similarity Index Measure (SSIM). Comparative methods included traditional and advanced approaches such as FBP, DIP, RED-CNN, FISTA, CascadeNet, and UPDNet.

CT Reconstruction:

• Low-Dose CT: The method was evaluated on low-dose CT data from the AAPM challenge dataset. The network was trained using images from 9 patients and evaluated on images from 1 patient. The proposed method did not require ground truth images for training, unlike competing methods such as DSM and RED-CNN.
• → Results: Figures 4 and 7 show that the proposed method outperformed traditional and supervised methods. It provided better tissue contrast and structural details, with a PSNR improvement of up to 4.62 dB over the DIP method.

• Sparse-View CT: Sparse-view data were generated from 720 views, reduced to 60 views for the experiment. The network was trained using only noisy data, while other methods required ground truth images.
• → Results: As illustrated in Figure 5, the proposed method reduced noise and artifacts more effectively than FBP and FISTA, achieving competitive PSNR and SSIM scores comparable to DSM while better restoring fine image structures.

Figure 4: low-dose CT results; top row reconstructed image, bottom row difference of the image to the ground truth

Figure 5: sparse-view CT results; top row reconstructed image, bottom row difference of the image to the ground truth

MRI Reconstruction:

• The method was validated using the fastMRI knee joint dataset. The training was performed on real-valued single-coil images, undersampled using a 4x acceleration rate and a Gaussian 1D mask.
• → Results: Figure 6 demonstrates the superior performance of the proposed method over traditional algorithms like L1Wavelet and SDE. The method provided clearer structures and fewer artifacts, with quantitative results confirming its robustness and effectiveness in reconstructing high-quality images from undersampled MRI data.

Figure 6: MRI reconstruction results with Gaussion 1D and Uniform 1D masks. Rows 1-3 and 4-6 each show one of the two image cases, two enlarged ROIs (knee joint and tissue), and difference images compared to the ground truth. respectively

Figure 7: Quantitative analysis of the proposed method against other state-of-the-art methods by PSNR and SSIM in three reconstruction tasks, including low-dose CT reconstruction, sparse-view CT reconstruction, and under-sampled MRI reconstruction with Gaussian 1D mask.

The proposed wavelet-improved SGM demonstrates significant advantages, such as robustness to noise, maintaining high reconstruction quality without ground truth images, and excelling in preserving fine details and structural information across various imaging modalities. Its unsupervised learning capability is particularly beneficial in clinical settings where clean ground truth data is scarce. However, the method incurs increased computational complexity and time due to the wavelet sub-network, posing a limitation for real-time applications. Additionally, it may struggle to recover very fine details under extreme imaging conditions, suggesting the need for further enhancements through integration with other reconstruction techniques.

3.2. 3D Shape generation

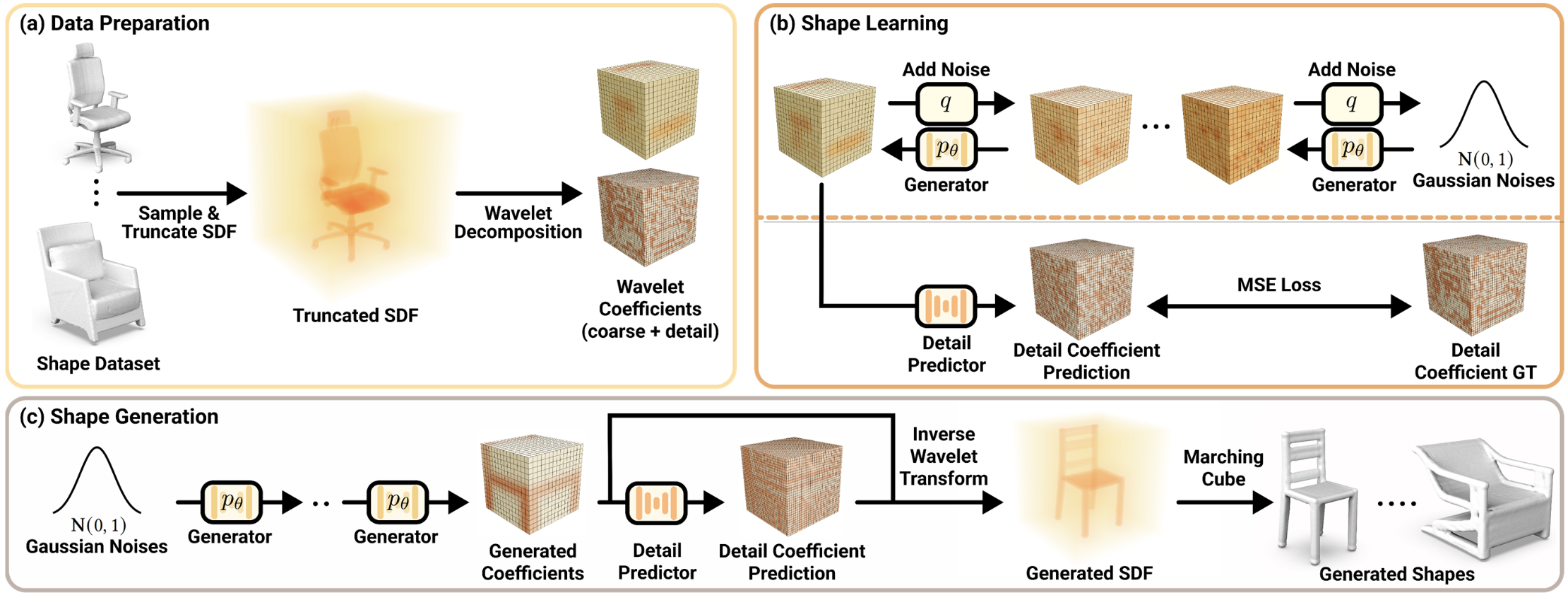
The second method is introduced in a paper titled "Neural Wavelet-domain Diffusion for 3D Shape Generation" [5] by Ka-Hei Hui and colleagues. It presents a novel approach for generating 3D shapes. This method addresses the limitations of existing generative models, which struggle to produce high-fidelity, diverse, and complex 3D shapes due to their reliance on voxel, point cloud, or mesh representations. The proposed solution leverages a continuous implicit representation in the wavelet domain, combining a compact wavelet representation with a pair of neural networks: a generator based on the diffusion model and a detail predictor. These innovations enable the generation of 3D shapes with fine details and clean surfaces, surpassing the capabilities of state-of-the-art models.

3.2.1. Method

The method revolves around three essential procedures: data preparation, shape learning, and shape generation, as shown in Figure 8.

(a) Data Preparation: This involves converting each input shape into a compact wavelet representation using truncated signed distance fields (TSDF) and multi-scale wavelet decomposition. This process results in a pair of coarse and detail coefficient volumes that effectively capture the shape's structure and details.

(b) Shape Learning: The shape learning phase trains two neural networks. Based on a denoising diffusion probabilistic model, the generator network generates coarse coefficient volumes from random noise. The detail predictor network then refines these coarse volumes by adding fine details, resulting in more realistic and intricate 3D shapes.

(c) Shape Generation: The trained generator network creates a coarse coefficient volume from a random noise sample. The detail predictor then adds fine details to this coarse volume. An inverse wavelet transform followed by the marching cube algorithm is used to reconstruct the final 3D shape.

Figure 8: Illustration of the proposed method in three stages (a) data preparation, (b) shape learning and (c) shape generation / inference

3.2.2. Experiments and Results

The experiments conducted in this paper aim to evaluate the performance of the proposed neural wavelet-domain diffusion method for 3D shape generation. The evaluation includes quantitative and qualitative comparisons against state-of-the-art methods such as IM-GAN, Voxel-GAN, Point-Diff, and SPAGHETTI.

For the Quantitative Evaluation, the authors used three metrics to assess the generated shapes:

• Minimum Matching Distance (MMD): Measures the fidelity of the generated shapes.
• Coverage (COV): Indicates how well the generated shapes cover the shapes in a given 3D repository.
• 1-NN Classifier Accuracy (1-NNA): Measures the ability of a classifier to differentiate the generated shapes from those in the repository.

Table 1 shows that the proposed method outperforms the other methods across most metrics for both the Chair and Airplane categories. Specifically in the chair category, the method achieved the highest COV (58.19), lowest MMD (11.70), and the most favorable 1-NNA (61.47) as well as in the airplane category, where it also excelled with a COV of 64.78, MMD of 3.230, and 1-NNA of 71.69. Therefore, the method generates shapes with higher fidelity and better coverage of the shape space while maintaining a balance that avoids overfitting.

Table 1: Quantitative comparison of the proposed method and other state-of-the-art methods evaluated on the chair and airplane categories.

For the Qualitative Evaluation, Figures 9 and 10, taken from the paper, showcase the generated shapes' visual quality. The proposed method produces shapes with complex structures, fine details, and clean surfaces without apparent artifacts. This is visually evident in the examples of tables, chairs, cabinets, and airplanes, which display intricate and challenging features that other methods struggle to replicate.

Figure 9: Selection of generated shapes, by the proposed methodFigure 10: Selection of generated shapes, by the proposed method compared to those generated by other state of the art methods

Additionally, the method was assessed over generating novel shapes rather than merely memorizing training data. Five hundred random shapes were generated and compared with training set shapes using Chamfer Distance (CD) and Light Field Distance (LFD). LFD, focusing on visual similarity, showed that the generated shapes shared similar structures but had noticeable local differences. Statistical analysis of the generated shapes' novelty using LFD revealed that the method produces both training-like and novel shapes. This indicates that it can generate realistic and diverse shapes not present in the training set.

An ablation study was conducted to further understand the contributions of different components. The results in Table 2 show that, first of all, the detail predictor significantly improves the generation quality across all metrics. Also, replacing the generator with a VAD model or directly predicting the TSDF leads to a performance decline, underscoring the importance of the diffusion model and wavelet representation.

Table 2: Quantitative results of the conducted ablation structure.

The proposed method offers several advantages, including high fidelity in generated shapes with detailed and realistic structures, effective coverage of a broad range of shapes, clean surfaces free from common artifacts, and realistic generation of novel shapes. However, as before, it has a high computational cost due to its iterative and interdependent process, which can result in long computing times despite the use of subsampling techniques. 

3.3. General Improvements in Generative Modeling

In their paper "Wavelet Score-Based Generative Modeling" [4], Guth et al. use a mathematical and numerical approach to analyze the computational effort for new data generation. They show that traditional SGMs require a high computational cost due to the many time steps needed to accurately discretize SDEs. The required time steps, therefore, depend mainly on the scale of the data, e.g., for image datasets on their size. By proposing the Wavelet Score-Based Generative Model (WSGM), they achieve significant computational efficiency, with the time complexity growing linearly with image size. The method is mathematically proven for Gaussian distributions and empirically validated for physical processes at phase transition and natural image datasets.

3.3.1. Method

Conceptually, their method is pretty straightforward, as shown in Figure 11. While the traditional SGM generates an image by directly using reverse diffusion to discretize noise into an image, a WSGM improves this process by working with wavelet coefficients at various levels of detail. It starts by using the SGM to create a basic, low-resolution image. Then, it generates wavelet coefficients conditional to this low-resolution image to enhance its detail. These wavelet coefficients are used to reconstruct a higher-resolution image through an inverse wavelet transform. This method is then repeated for each level of detail. Importantly, WSGM requires the same number of steps at each level, which are significantly fewer than those needed for a traditional SGM, making it much more efficient.

Figure 11: Illustration of a regular SGM model on top and the proposed WSGM model on the bottom

Additionally, the paper goes on to mathematically prove certain theorems to show that using the wavelet transform significantly impacts the number of diffusion steps required, making them independent of the input data size.

For this purpose, three theorems are formulated and proven. The complete mathematical formulations can be found in [4] for interested readers.

Theorem 1 provides an upper bound on the Kullback-Leibler (KL) divergence error between a Gaussian distribution $//<![CDATA[ \begin{array}{l}\mathcal{N}(0, \Sigma)\end{array} //]]>$ and its discretized version $//<![CDATA[ \begin{array}{l}\tilde{p}_0\end{array} //]]>$ after time $//<![CDATA[ \begin{array}{l}T\end{array} //]]>$ with discretization $//<![CDATA[ \begin{array}{l}\delta_k = \delta\end{array} //]]>$. 

The theorem states that for any $//<![CDATA[ \begin{array}{l}\epsilon > 0\end{array} //]]>$, there exist $//<![CDATA[ \begin{array}{l}T\end{array} //]]>$ and $//<![CDATA[ \begin{array}{l}\delta\end{array} //]]>$ such that:

$//<![CDATA[ \begin{array}{l}\left( \frac{1}{d} \right) (E_T + E_\delta) \leq \epsilon \quad \text{and} \quad N = \frac{T}{\delta} \leq C \epsilon^{-2} \kappa^3,\end{array} //]]>$

With $//<![CDATA[ \begin{array}{l}C \geq 0\end{array} //]]>$ being a universal constant and $//<![CDATA[ \begin{array}{l}\kappa\end{array} //]]>$ the conditioning number of $//<![CDATA[ \begin{array}{l}\Sigma\end{array} //]]>$.

This means that the number of time steps $//<![CDATA[ \begin{array}{l}N\end{array} //]]>$ needed to achieve a KL error $//<![CDATA[ \begin{array}{l}\epsilon\end{array} //]]>$ increases with the condition number $//<![CDATA[ \begin{array}{l}\kappa\end{array} //]]>$of $//<![CDATA[ \begin{array}{l}\Sigma\end{array} //]]>$. For stationary processes, where the covariance eigenvalues follow a power spectrum decay, $//<![CDATA[ \begin{array}{l}\kappa\end{array} //]]>$ is proportional to the image size, indicating $//<![CDATA[ \begin{array}{l}N\end{array} //]]>$ must increase with the image size.

Theorem 2 provides a more general bound on the total variation distance between a probability distribution $//<![CDATA[ \begin{array}{l}p\end{array} //]]>$ and its discretized version $//<![CDATA[ \begin{array}{l}\tilde{p}_0\end{array} //]]>$, extending to non-Gaussian processes. It considers the log density's regularity  $//<![CDATA[ \begin{array}{l}\log p_t(x)\end{array} //]]>$ over time $//<![CDATA[ \begin{array}{l}t\end{array} //]]>$ and space $//<![CDATA[ \begin{array}{l}x\end{array} //]]>$, depending on constants $//<![CDATA[ \begin{array}{l}K\end{array} //]]>$ and $//<![CDATA[ \begin{array}{l}M\end{array} //]]>$. The calculated bound shows that the approximation error is controlled by the regularity constants $//<![CDATA[ \begin{array}{l}K\end{array} //]]>$ and $//<![CDATA[ \begin{array}{l}M\end{array} //]]>$, eliminating exponential growth with $//<![CDATA[ \begin{array}{l}T\end{array} //]]>$. It indicates that a well-conditioned covariance matrix is crucial to minimize error, and non-Gaussian processes with ill-conditioned covariance matrices may require more discretization steps to achieve a small error.

Theorem 3 provides results in the context of a Gaussian multi-scale process, giving explicit bounds for the convergence and error rates of the proposed WSGM method. Using this method, they come to a different upper bound, stating that for any $//<![CDATA[ \begin{array}{l}\epsilon > 0\end{array} //]]>$, there exist $//<![CDATA[ \begin{array}{l}T\end{array} //]]>$ and $//<![CDATA[ \begin{array}{l}\delta\end{array} //]]>$ such that:

$//<![CDATA[ \begin{array}{l}\left( \frac{1}{d} \right) (E_T + E_\delta) \leq \epsilon \quad \text{and} \quad N = \frac{T}{\delta} \leq C \epsilon^{-2}.\end{array} //]]>$

The number of diffusion steps required to reach a fixed error is now independent of the input data size (e.g., image size), as the bound is no longer dependent on the conditioning number $//<![CDATA[ \begin{array}{l}\kappa\end{array} //]]>$ of  $//<![CDATA[ \begin{array}{l}\Sigma\end{array} //]]>$. This result is shown in the Gaussian process setting but indicates more general applicability.

3.3.2. Experiments and Results

Three experiments were conducted: (1) For Gaussian multi-scale processes, WSGM demonstrated linear time complexity and dimension-independent conditioning numbers, outperforming SGMs. (Figure 12) (2) On physical processes, particularly the critical $//<![CDATA[ \begin{array}{l}\phi^4\end{array} //]]>$ model, WSGM showed significantly reduced errors and better scalability than SGMs. (Figure 13) (3) When tested on high-resolution natural images from the CelebA-HQ dataset, WSGM achieved superior perceptual quality with fewer steps and lower Fréchet Inception Distance (FID) scores compared to SGMs. These results highlight WSGM's efficiency and scalability across different types of data. (Figure 14)

WSGMs offer notable advantages, including efficiency through fewer iterations to reach desired accuracy, scalability in handling high-resolution images while maintaining performance, and superior perceptual quality in generated images, as lower FID scores indicate. However, the method's complexity is a significant drawback, as it involves integrating wavelet transforms and managing conditional distributions of wavelet coefficients. Additionally, the method is mainly effective for multi-scale processes with near-Gaussian conditional distributions, and extending it to non-Gaussian processes may necessitate further techniques.

Figure 12: Quantitative comparison of SGM and WSGM. Left and middle: error on the estimated covariance matrix w.r.t. the number of discretization steps (one step has size T=10); Right: number of discretization steps required to reach a fixed error ε = 0.1 w.r.t. the image size

Figure 13: Left: Error comparison between ground-truth datasets and synthesized datasets (SGM and WSGM) across different dimensions (L) and discretization steps. Middle: Visual samples of ground truth (top) and WSGM (bottom). Right: Power spectrum of ground truth for L = 32.

Figure 14: Top. Left: SGM generations with 16 discretization steps. Middle: WSGM generations with 16 discretization steps per scale. Right: Power spectrum of CelebA-HQ. Bottom. Left: FID evolution vs. diffusion steps for SGM and WSGM with L = 128. Middle: FID evolution vs. diffusion steps for SGM at different image sizes L. Right: FID evolution vs. diffusion steps for WSGM at different image sizes L.

4. Discussion

All three methods leverage wavelet transforms in distinct ways, demonstrating their ability to enhance generative models by effectively handling multi-scale data and capturing fine details. This capability ensures high fidelity, preserving intricate structures and improving overall image quality. Each method also shows robustness in various applications, whether handling noisy training data, maintaining performance across different scales, or achieving better perceptual quality. However, incorporating wavelet transforms increases system complexity, potentially leading to longer computation times and limiting their suitability for all situations.

Combining insights from the three studies, wavelet-enhanced diffusion models show significant promise in medical imaging. The independence of generated image size demonstrated by WSGMs provides a substantial advantage when generating extensive datasets of high-quality medical images, potentially reducing computation time. Operating unsupervised while preserving fine details and showing less sensitivity to artifacts offers significant benefits in clinical settings where clean ground truth data may not be available. The qualitative results from wavelet-enhanced 3D shape generation suggest great potential for generating diverse 3D datasets of smooth anatomical structures.

These methods collectively represent significant advancements in leveraging wavelet transforms for improved image processing. Their ability to enhance detail recovery, reduce noise, and maintain high perceptual quality makes them invaluable in applications ranging from CT and MRI reconstructions to generating realistic shapes. However, the trade-offs between computational efficiency, implementation complexity, and robustness to various data conditions must be carefully considered. Future research could focus on integrating the strengths of these methods while mitigating their limitations, potentially through hybrid approaches that combine wavelet transforms with other advanced techniques to handle a broader range of image processing challenges. For example, extending WSGMs to 3D might leverage increased computational efficiency and superior shape generation ability. Interesting would also be how the proposed methods would perform on ultrasound images, which remains the noisiest and blurriest of the imaging modalities.

While I was not initially aware of the potential use cases of wavelet transforms as an enhancement for diffusion models, I can see great potential in the research I have encountered during this project. So, I can only encourage further research in this promising area.

5. References

[1] Celard P, Iglesias EL, Sorribes-Fdez JM, Romero R, Vieira AS, Borrajo L. A survey on deep learning applied to medical images: from simple artificial neural networks to generative models. Neural Comput Appl. 2023;35(3):2291-2323. doi:10.1007/s00521-022-07953-4

[2] Croitoru, F. A., Hondru, V., Ionescu, R. T., & Shah, M. (2023). Diffusion models in vision: A survey. IEEE Transactions on Pattern Analysis and Machine Intelligence.

[3] Donoho, D. L. (1995). De-noising by soft-thresholding. IEEE transactions on information theory, 41(3), 613-627.

[4] Guth, F., Coste, S., De Bortoli, V., & Mallat, S. (2022). Wavelet score-based generative modeling. Advances in Neural Information Processing Systems, 35, 478-491.

[5] Hui, K. H., Li, R., Hu, J., & Fu, C. W. (2022, November). Neural wavelet-domain diffusion for 3d shape generation. In SIGGRAPH Asia 2022 Conference Papers (pp. 1-9).

[6] K. Kim, G. El Fakhri, and Q. Li, “Low-dose CT reconstruction using spatially encoded nonlocal penalty,” Med. Phys., vol. 44, no. 10, pp. e376–e390, Oct. 2017.

[7] Pinto-Coelho L. How Artificial Intelligence Is Shaping Medical Imaging Technology: A Survey of Innovations and Applications. Bioengineering. 2023; 10(12):1435. https://doi.org/10.3390/bioengineering10121435

[8] S. Niu et al., “Sparse-view X-ray CT reconstruction via total generalized variation regularization,” Phys. Med. Biol., vol. 59, no. 12, pp. 2997–3017, Jun. 2014.

[9] Shin, Y. H., Park, M. J., Lee, O. Y., & Kim, J. O. (2020). Deep orthogonal transform feature for image denoising. IEEE Access, 8, 66898-66909.

[10] Sifuzzaman, M., Islam, M. R., & Ali, M. Z. (2009). Application of wavelet transform and its advantages compared to Fourier transform.

[11] Song, Y., Sohl-Dickstein, J., Kingma, D. P., Kumar, A., Ermon, S., & Poole, B. (2020). Score-based generative modeling through stochastic differential equations. arXiv preprint arXiv:2011.13456.

[12] Walker, J. S., & Nguyen, T. Q. (2001). Wavelet-based image compression. Sub-chapter of CRC Press book: Transforms and Data Compression, 267-312.

[13] Wu, W., Wang, Y., Liu, Q., Wang, G., & Zhang, J. (2023). Wavelet-improved score-based generative model for medical imaging. IEEE transactions on medical imaging.