Abstract
Knowledge graphs serve as structured repositories of information, but their static nature limits their applicability in dynamic environments. The emergence of Temporal Knowledge Graphs (TKGs), represented as quadruples (subject, relation, object, timestamp), addresses this limitation by introducing the temporal dimension. This blog post delves into the realm of link prediction methods for TKGs, aiming to forecast future relationships between entities.
Outline
- Introduction
- Motivation
- Models and Frameworks
- MOST
- CyGnet
- GenTKG
- Comparison
- Personal Review
- References
1. Introduction
Knowledge graphs serve as powerful repositories of information, presenting data in structured triplets that form the backbone of various artificial systems such as recommendation engines and question-answering frameworks. Coined in 1973 by an Austrian linguist, the visual representation of knowledge graphs in Figure 1 vividly illustrates entities as nodes and relationships as edges. However, a fundamental challenge arises - knowledge graphs inherently capture a static snapshot of facts. In a dynamic world where information evolves over time, the static nature of traditional knowledge graphs becomes a limitation. Facts, as we know them, are not immutable; they undergo transformations, updates, and modifications.
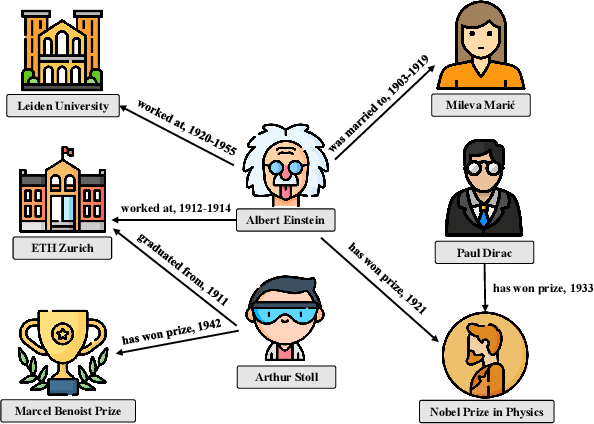
To address this limitation, the concept of Temporal Knowledge Graphs (TKGs) emerges, incorporating the crucial element of time into the information architecture. In a TKG, each fact is represented as a quadruple (s, r, o, t), where 't' denotes the timestamp specifying the temporal validity of the fact. This innovation allows us to contextualize information within a specific timeframe, acknowledging the dynamic nature of evolving data. In Figure 2, we observe a TKG example where information is structured in quadruples. This representation elegantly captures the essence of temporal evolution in data. Notably, Representative TKGs such as the Global Database of Events, Language, and Tone (GDELT) and Integrated Crisis Early Warning System (ICEWS) exemplify the practical application of TKGs in real-world scenarios.
2. Motivation
In light of our preceding discussion, let's now delve into the core question: why does it matter? How do Temporal Knowledge Graphs (TKGs) significantly influence the domain of medical applications?[1] navigates through the challenges in constructing a medical knowledge graph, drawing from Electronic Health Records (EHR) data and underscoring the complexities inherent in this process. Yet, once this medical knowledge graph is crafted, its potential applications emerge as groundbreaking. Take, for instance:
Medication Recommendation: TKGs, curated from EHR data, become instrumental in healthcare recommendation systems, especially in the context of medication recommendations.Through a meticulous analysis of patient details, diseases, medications, and diagnoses, the TKG can empower a sophisticated recommendation framework.
Disease Diagnosis: Medical knowledge graphs can leverage diverse data sources such as medical images, EHR data, and clinical notes, to classify diseases.
Adverse Drug Event Detection: TKGs can play a crucial role in detecting adverse drug events by predicting unknown drug reactions and inferring previously undiscovered connections within the graph.
beyond these core applications, the versatility of TKGs extends into areas such as predictive analysis, question answering, and more. This multifaceted approach highlights the profound impact that TKGs can have on shaping the future of healthcare analytics.
TKGs are known to be incomplete, they exhibit incompleteness due to various reasons like , dynamic nature of the world, data collection challenges and temporal aspects. Also , we are usualy interested in future relationship forecasting. In dynamic environments, relationships between entities evolve over time. Link prediction models can forecast future relationships based on historical patterns, enabling TKGs to capture evolving dynamics and stay up-to-date. This is particularly relevant in applications where understanding future interactions is essential.
Developing a link prediction model for Temporal Knowledge Graphs (TKGs) can help address the issue of incompleteness in TKGs by predicting missing relationships or links between entities. That brings us to the question of, what exactly is link prediction? Link prediction is a task in the field of machine learning and network analysis where the goal is to predict the likelihood or existence of connections (links or edges) between entities in a given network. In the context of Temporal Knowledge Graphs (TKGs), link prediction specifically involves predicting temporal relationships between entities at different timestamps. Each relationship is typically represented as a quadruple (subject, relation, object, timestamp). The objective is to infer or predict missing relationships over time, given the observed temporal patterns in the data.
Let's consider a scenario in the domain of biomedical research where a Temporal Knowledge Graph (TKG) is used to represent relationships between genes, diseases, and related events.suppose we have the following information in our TKG:
- (GeneA, AssociatedWith, DiseaseX, 2020)
- (GeneB, InteractsWith, GeneC, 2021)
- (DrugY, Targets, GeneA, 2022)
Now, due to the dynamic nature of biological processes, there might be missing relationships or events that are not explicitly mentioned in the TKG. A link prediction model can help predict potential missing links. Link Prediction Result: The model predicts a new relationship - (GeneB, AssociatedWith, DiseaseX, 2022). in this case, the link prediction model inferred a potential association between GeneB and DiseaseX based on patterns observed in the existing TKG. This prediction helps address the incompleteness of the TKG by suggesting a relationship that wasn't explicitly stated but could be plausible based on the temporal dependencies observed in the data.
In this blog post, we will explore three cutting-edge algorithms and related concepts for link prediction.
3. Models and Frameworks
3.1. MOST
3.1.1. Background
According to [2], it has been found that a large portion of KG and TKG relations are sparse. Basically many relations in Knowledge Graphs (KG) and Temporal Knowledge Graphs (TKG) have limited occurrences, indicating that these relations are not widely distributed or common. In other words, there are a few relations that occur frequently and are well-represented in the KG or TKG, while the majority of relations happen infrequently, forming a long-tail distribution. This problem leads to the degenerated link inference performance of the traditional KG and TKG reasoning methods.
Based on [2], the link prediction task can be classified into two distinct approaches:
Interpolated LP Task: Interpolation involves making predictions within the observed or known data points. It means predicting links for relations that may not have been explicitly mentioned but are considered to be within the range or spectrum of observed relations.
Extrapolated LP Task: In contrast to interpolation, extrapolation involves making predictions outside the observed data points. It means predicting links for relations that are not present in the observed data.
According to [2], existing methods face challenges in extrapolated and interpolated predictions, with the best-performing ones excelling at interpolation but falling short in extrapolation. Flaws in previous approaches include a focus on predicting missing object entities, neglecting subject entities, and issues with databases, such as sparse relations with minimal associated quadruples.[2] aims to overcome these limitations by providing a comprehensive solution that addresses both extrapolation and interpolation challenges, emphasising on both missing subject and object entities, and improving handling of sparse relations by considering the unique characteristics of relations with minimal observed instances. [2] refers to TKG interpolated LP as TKG completion, while TKG extrapolated LP is alternatively known as TKG forecasting or TKG link forecasting and the paper defines them as following:
One-shot TKG Interpolated link prediction: It involves predicting missing entities in link prediction queries based on a single observed quadruple for each sparse relation. In this scenario, we're dealing with limited clues, where only one piece of information (quadruple) is available for uncommon relations. The goal is to make predictions within the range of observed relations, not extending into the future. So given (s0,r,o0,t0) and the whole background graph G′, one-shot TKG interpolated LP aims to predict the missing entity of each LP query, i.e., (sq,r,?,tq)or (?,r,oq,tq) [2].
One-Shot TKG Extrapolated Link Prediction): Similar to the previous case, assume that for each sparse relation only one quadruple In contrast to interpolation, extrapolation involves making predictions outside the observed data points. Here, the focus is on predicting links for relations that are not present in the observed data but are in the future. So given (s0,r,o0,t0), together with a set of observed TKG facts that appear prior to t0 and belong to the background graph G ′, one-shot TKG extrapolated LP aims to predict the missing entity of each LP query, i.e., (sq , r, ?, tq ) or (?, r, oq , tq ).
3.1.2. Method
In figure 3 , we are presented with a conceptual overview of the model's functioning.
The proposed model MOST, is composed of 4 different stages, explained as followed:
3.1.2.1. Meta-information extractor: The objective of this part is to Extract meta-information about a sparse relation (r) from its support entities (s0, o0). The time aware entity representations h(s0 ,t0 ) , h(o0 ,t0 ) of s0, o0 are derived according to formula 1, where N ̃s0 and N ̃o0 represents the filtered neighborhood , d is the dimnetion of representations and Wg is a weighted matrix that processes the information in graph agreggation. f is a layer of feed-forward neural network. δ1 is a triangle parameter deciding how much information from the temporal neighbours is included in updating entity presentation and σ is an activation function. (This information has been replicated exactly from the formula explanation in the referenced paper [2])
3.1.2.2. Meta-representation learner: Derives the meta-representation (hr) of the sparse relation r based on the extracted meta-information according to formula 2. In the formula, fproj, f1r and f2r are three single layer neural networks.
3.1.2.3. Metric function: Computes the plausibility scores for query quadruples related to the sparse relation r according to formula 3. hsq ∈ Rd and hoq ∈ Rd denote the time-invariant entity repre- sentations of sq and oq , respectively. δ2 is a trainable parameter controlling the amount of injected temporal information.
3.1.2.4. Parameter learning(Episode training): Trains the model's parameters iteratively through episodic training cycle learning from both support and query example according to formula 4. where lg and lq- denote the binary cross entropy loss of q and q-, respectively.
3.1.3. Performance Result
MOST generates its datasets by filtering data from ICEWS and GDELT for comparison. It then develops two distinct models, one for interpolation and another for extrapolation. While delving into these details might be confusing, it's essential to note that their proposed method consistently outperformed the majority of other methods (presented by them)in various scenarios.
3.2. CyGNet
3.2.1. Background
The basic idea behind this model is that temporal facts in knowledge graphs evolve over time.[3] Notably, many facts exhibit recurring patterns along the timeline, such as occurrences of economic crises and diplomatic activities.More specifically, the paper argues that over 80% of all the events throughout the 24 years of ICEWS data (i.e. 1995 to 2019) have already appeared during the previous time period. This insight suggests that a model can gain valuable insights from historical data, leveraging known facts to enhance its learning capabilities.
Existing methods often overlook these evolution patterns in TKGs. CyGNet is designed to predict future facts while considering recurrence patterns in TKGs. CyGNet is inspired by the copy mechanism.
The copy mechanism, previously applied in Natural Language Generation (NLG) tasks like abstractive summarization, involves selecting output directly from the input sequence. This mechanism has not been previously applied to Temporal KGs so CyGNet is the first model to incorporate this mechanism into modelling TKGs.
3.2.2. Method
The goal here is to predict the missing object entity given a temporal fact in the form (s, p, ?, t). But the model can easily be extended to predict other entities like the subject entity. CyGNet model combines two modes of inference, namely Copy mode and Generation mode. I will try to explain how CyGnet works through an example as well.
Assume we have historical snapshots spanning time steps t1 to tT, capturing facts in a temporal knowledge graph. G(t1, tT) represents the known facts in these snapshots. We want to predict a future fact for the quadruple (s1, p3, ?, T + 1). Assume that entities related to (s1, p3) in historical snapshots are {s3, s4, s5, ..., sm}. The Entire entity vocabulary is {e1, e2, ..., en} , and, of course, includes all the entities, i.e., s1, s2, s3, .... .
3.2.2.1. Copy mode: It is designed to identify entities that have appeared in the historical data, indicating a repetition or recurrence of facts over time. So the model in copy mode selects entities from a specific historical vocabulary that is tailored to a particular subject entity, predicate, and time step. This historical vocabulary includes entities that have been observed recurrently as object entities in facts involving the given subject entity and predicate at earlier time steps. This mode is particularly useful for predicting entities that are likely to repeat based on historical patterns.
In formula 5, the term tk is updated based on the previous time step tk−1 and a temporal update tu. . The index vector vq is then generated using a hyperbolic tangent activation function applied to the weighted sum of subject entity s, predicate p, and time step tk contributing to the Copy mode's mechanism in enhancing the probability estimation for object entities from the historical vocabulary.
The objective of the copy mode in the example would be to estimate the probability of entities from the historical vocabulary {s3, s4, s5, ..., sm}. These entities have historically served as object entities for the subject entity s1 and predicate p3 in the known snapshots G(t1, tT). So If s4 frequently appeared as an object entity for (s1, p3) in the past snapshots, the copy mode would assign a higher probability to s4 for the current time step (T + 1).
3.2.2.2. Generation mode:This mode aims to predict entities from the entire entity vocabulary, considering the complete set of possible entities without being restricted to historical patterns. The model in generation mode predicts entities without explicitly relying on the historical context. It generates predictions based on the general knowledge of the entire entity space, not limited to the entities that have repeated in history. This mode is more versatile and can be effective for predicting entities that may not have repeated in history but are still valid predictions based on overall knowledge.
According to formula 6, The Generation mode involves the generation of an index vector gq, achieved through a softmax function applied to the weighted sum of subject entity s, predicate p, and time step tk . Then the softmax function is applied to gq to obtain p(g), representing the predicted probabilities across the entire entity vocabulary. Analogous to p(c) in the Copy mode, p(g) signifies the model's estimation of probabilities for the entire entity set. The maximum value within p(g) corresponds to the object entity predicted by the model in the comprehensive entity vocabulary.
The objective of the Generation mode in our example is to estimate the probability of every entity in the entire entity vocabulary {e1, e2, ..., en}. This mode considers the overall knowledge of entities without specific historical constraints. It might assign probabilities to entities based on general patterns in the entire knowledge graph, regardless of their historical association with (s1, p3).
**CyGNet combines the probabilistic prediction , from both Copy mode and Generation mode to output the final prediction.
According to Formula 7, In the integration process, CyGNet dynamically adjusts the weight between the Copy mode and the Generation mode through a tunable parameter α. The parameter α is constrained to the range [0,1][0,1], ensuring a valid interpolation between the Copy mode (p(c)) and the Generation mode (p(g)).
The model combines the probabilities estimated by the Copy mode (historical context) and the Generation mode (overall knowledge) to make a comprehensive prediction for the missing object entity in the quadruple (s1, p3, ?, T + 1).This combined prediction leverages both historical recurrence patterns and general knowledge for a more informed estimation of the missing entity in the future fact.
Figure 4 depicts CyGNet's copy-generation mechanism in action. Taking the example of predicting the NBA champion in 2018, CyGNet acquires embedding vectors for each entity (represented by the color bar). It employs both inference modes to determine entity probabilities, shown as green bars, considering historical context or the entire entity vocabulary. Notably, "Golden State Warriors" is present in both Copy and Generation modes
3.2.3. Performance Result
The paper utilizes five benchmark datasets, as outlined in Table 1, to evaluate the performance of the CyGen model across various scenarios.
Table 2 displays the performance results for three of those benchmarking datasets, revealing that CyGen consistently outperforms similar models.
3.3. GenTKG
3.3.1. Background
GENTKG aims to leverage large language models (LLMs) for temporal knowledge forecasting in TKGs. The goal here is to bring temporal knowledge forecasting into the generative setting, where the model generates predictions based on temporal relational data. There are two major challenges here, First one would be the gaps between the complex temporal graph data structure and the sequential natural expressions that LLMs can handle. Handling complex temporal multi-relational graph data, like TKGs with tens of thousands of quadruples, becomes difficult when trying to make it compatible with the sequential language understanding abilities of LLMs. Second challenge is dealing with the large data sizes of TKGs and the heavy computation costs associated with fine-tuning LLMs. As a result, GenTKG is proposed as a framework to leverage LLMs for generative forecasting on temporal knowledge graphs, addressing challenges in data structure and computation costs.[4]
3.3.2. Method
This framework leverages a two-step approach to improve the alignment of Large Language Models (LLMs) with the task of generative forecasting on TKGs.
3.3.2.1. Retrieve Phase
The first challenge, related to the modality difference between structured temporal graph data and sequential natural languages, is tackled in the retrieval phase of GenTKG.
In essence, the retrieval phase involves learning logical rules from the TKG, applying these rules to identify relevant historical events, converting these events into natural language prompts, and then using these prompts as input for an LLM. This process enables the LLM to comprehend the structured temporal relational data from the TKG. Although the prompts are in the form of sequential natural languages, they implicitly carry structural information from the TKG. These prompts enable LLMs to comprehend temporal relational data, and this comprehension is not dependent on the specific LLM backbone being used.
Formula 7, represents a probability distribution used in the retrieval phase of GenTKG. Here, P(u;e2,t) is the probability of transitioning to entityu given the current entity e2 and time t. The numerator exp(tu−t) is the exponential of the time difference between the target entity u and the current time t. The denominator sums the exponential time differences for all candidate entities u′ adjacent to the current entity e2 at time t, creating a normalized distribution that prioritizes entities closer in time during the sampling process
3.3.2.2. Generate Phase
The generation phase tackles the challenge of high computation costs associated with training Large Language Models (LLMs) on huge temporal knowledge graph (TKG) dataset.
GenTKG employs a parameter-efficient fine-tuning (PEFT) adaptation method called Low-rank Adaptation (LoRA). This approach aims to address the high computation costs and hardware requirements associated with training LLMs. LoRA is specifically designed to provide efficient fine-tuning, allowing GenTKG to adapt pre-trained LLMs for the task of TKG forecasting without requiring extensive computational resources. The use of parameter-efficient instruction tuning contributes to outperforming many other approaches in TKG forecasting tasks.
3.3.3. Performance Result
This study employs five benchmark datasets, as detailed in Table 3, to assess the performance of the GenTKG model under diverse scenarios.
As depicted in table 5, the application of GenTKG with a robust language model demonstrates superior performance compared to the majority of models in their benchmark datasets.
4. Comparison
While the benchmarking methods of the first model, MOST, differ from those of CyGNet and GENTKG, there is a common ground for comparison between CyGNet and GENTKG. Both CyGNet and GENTKG undergo benchmarking on the ICEWS18 dataset, enabling a meaningful comparison between these two methods.
According to Table 5 , CyGNet outperforms GenTKG(+Llama2-7B) across all evaluation metrics on the ICEWS18 dataset. Specifically, CyGNet shows a significantly higher accuracy in predicting the correct entities at the top ranks, as indicated by the superior performance in Hits@1, Hits@3, and Hits@10 when compared to GenTKG(+Llama2-7B). These results suggest that, based on the ICEWS18 dataset, CyGNet demonstrates a notably better predictive capability than GenTKG(+Llama2-7B).
5. Personal review
Having navigated through the intricacies of Temporal Knowledge Graphs (TKGs) and explored the promising link prediction models, I find myself intrigued by the transformative potential and the evolving landscape of this concept. Here are my personal reflections:
5.1. Model Oversell
A notable aspect that caught my attention is the careful consideration needed in the comparative evaluation since there is a subtle sense of overselling the models. The papers appear to position the proposed models as superior, often comparing them against alternatives that may not be optimal benchmarks. In several instances, models with inferior performance are chosen for comparison, creating a potentially skewed perspective on the effectiveness of the proposed approaches. It's crucial to approach these comparisons with discernment, recognizing the need for fair and representative benchmarks. As a reader, this prompts me to be mindful of the nuanced details in the comparative analysis and encourages a more critical examination of the models' performance against a diverse set of benchmark.
5.2. Strange Mistakes: Questioning The Foundation
A peculiar anomaly caught my attention in the MOST paper, raising questions about the foundational premise. The paper asserts that a large portion of Knowledge Graph (KG) and Temporal Knowledge Graph (TKG) relations are sparse, citing a reference that focuses on KGs, specifically Wikidata. The reference discusses the sparsity of relations in Wikidata, a conventional KG, without explicitly addressing TKGs. One plausible explanation suggested by a colleague during my presentation involves the consideration of clusters as a single occurrence. However, the paper explicitly states that these relations are long-tail and only occur a few times, making it less likely that the mistake stems from treating clusters as a unit. This anomaly prompts a critical examination of the paper's foundational assumptions, urging readers to approach the presented information with a cautious eye. It serves as a reminder of the importance of rigorous fact-checking, particularly when establishing the groundwork for novel concepts like Temporal Knowledge Graphs.
5.3. Promising Field
The exploration of Temporal Knowledge Graphs (TKGs) within the realm of healthcare, particularly leveraging Electronic Health Records (EHR) data, unfolds a promising frontier with immense potential. Notably, the focus on applications such as Medication Recommendation and Disease Diagnosis within the healthcare domain underscores the transformative impact TKGs can have on clinical decision-making processes. As a reader actively engaged in research, the scarcity of papers on medical knowledge graphs resonates as a testament to the untapped opportunities within this domain. The dearth of existing literature signifies a vast and open field for exploration, encouraging researchers to delve into uncharted territories and contribute to the theoretical foundations of medical knowledge graphs.
5.4. Revolutionary Potential
The revolutionary potential of TKGs, coupled with advanced link prediction models, becomes evident. The ability to forecast future relationships in dynamic environments, holds the promise of transforming how we perceive and utilize healthcare data.
5.5. Still A Long Way Ahead
Despite the strides made in TKGs and link prediction models, it's evident that we are still on a journey with much ground to cover. The incompleteness challenges, data collection limitations, and the dynamic nature of the real world remind us that there's a long way ahead in achieving the full potential of these frameworks.
6. References
[1] Lino Murali, G. Gopakumar, Daleesha M. Viswanathan, Prema Nedungadi, Towards electronic health record-based medical knowledge graph construction, completion, and applications: A literature study, Journal of Biomedical Informatics, Volume 143, 2023,104403,ISSN 1532-0464
[2] Ding, Z., He, B., Wu, J., Ma, Y., Han, Z., & Tresp, V. (2023). Learning Meta-Representations of One-shot Relations for Temporal Knowledge Graph Link Prediction. arXiv preprint arXiv:2205.10621v2 [cs.LG], submitted on 24 May 2023. https://arxiv.org/pdf/2205.10621.pdf
[3] Zhu, C., Chen, M., Fan, C., Cheng, G., & Zhang, Y. (2020). Learning from History: Modeling Temporal Knowledge Graphs with Sequential Copy-Generation Networks. arXiv preprint arXiv:2012.08944, v1 submitted on 15 Dec 2020, last revised v2 on 5 Mar 2021 https://ojs.aaai.org/index.php/AAAI/article/view/16604/16411
[4] Liao, R., Jia, X., Ma, Y., & Tresp, V. (2023). GENTKG: Generative Forecasting on Temporal Knowledge Graph. arXiv preprint arXiv:2310.07793v2 [cs.CL], submitted on 14 Nov 2023. https://arxiv.org/pdf/2310.07793.pdf