Model Order Reduction for Optimization

Authors: Isabel Keller, Torsten Schmid

Supervisors: Sebastian Schopper, Lukas Kleine-Wächter

Motivation for Model Order Reduction for Optimization

Model order reduction (MOR) techniques offer the possibility to reduce the computational cost for the solution of large systems while keeping the necessary accuracy. MOR can be especially advantageous if repetitive evaluation of those large systems is needed like it is the case in optimization or reliability assessment.

Parametric model order reduction methods (pMOR) are able to deal with the changes of the system parameters. So the model order reduction technique is only applied once before the optimization and the whole optimization process is conducted using this parametric model. In the following investigations, this more sophisticated technique is not used. Instead, for every new set of parameters a new basis and therefore or new reduced-order model (ROM) is constructed.

Basics of applied Model Order Reduction techniques

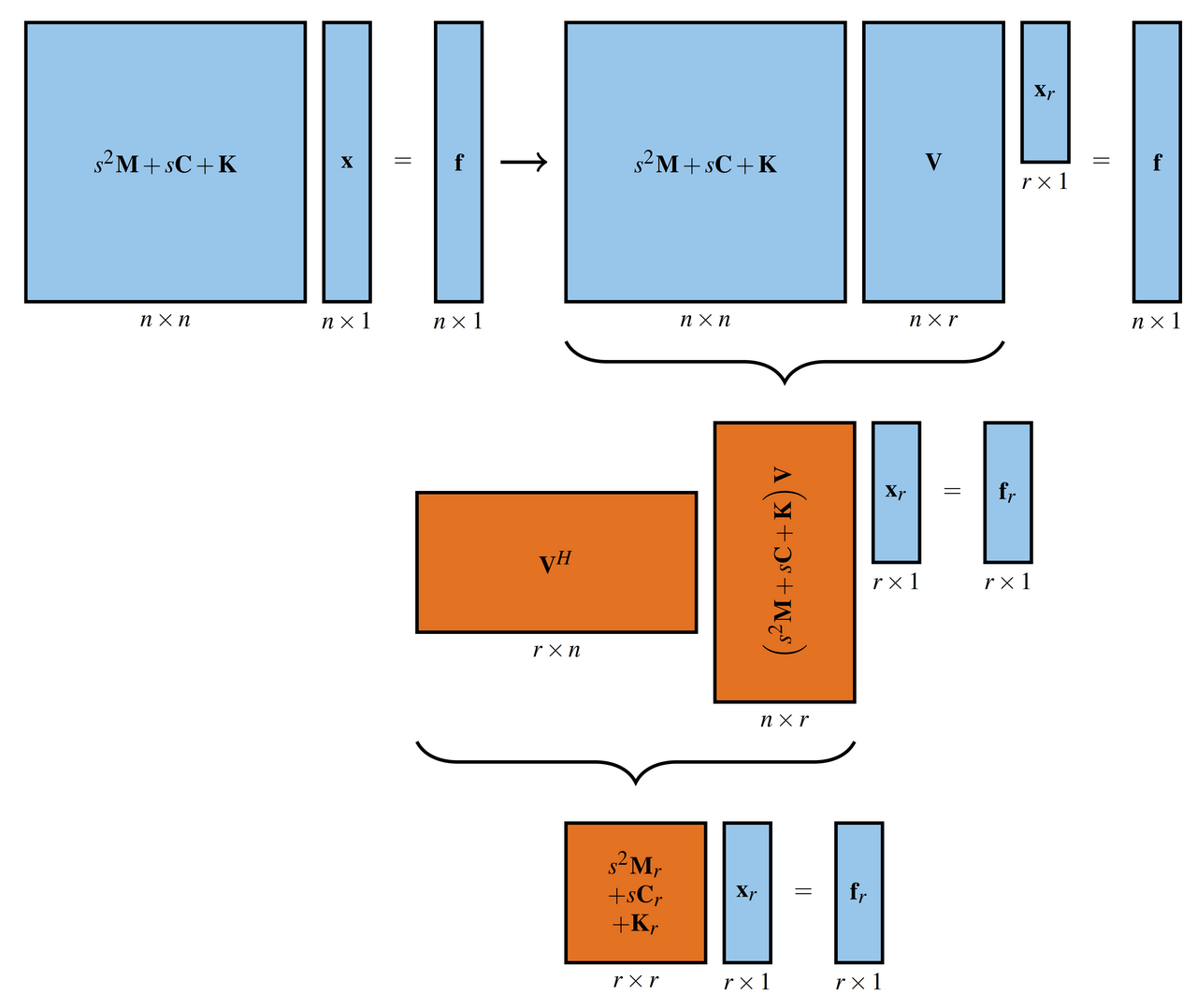
Like a lot of model order reduction techniques, the used methods are projection-based i.e, they construct by a certain procedure a projection matrix, that is used to obtain an equation system of lower dimensionality. The principal difference between those methods is how they construct the projection matrix.

The projection step is usually the same: the system matrices are left and right multiplied with projection matrices. If for both multiplications the same matrix is used this is referred to as a Galerkin projection or a one-sided projection. Another possibility is to use different matrices for the right and left multiplication, which is known as a Petrov-Galerkin projection or a two-sided projection. For the following investigations, a one-sided projection was used.

Figure 1: Projection procedure [1]

The following model order reduction methods were used:

• Proper orthogonal decomposition (POD)

• Krylov-Galerkin projection

Proper orthogonal decomposition (POD)

The basic idea of this method is to construct a basis for the projection by collecting displacement samples of the full order model for given sampling frequencies. These samples are stored in the so-called snapshot matrix, which has the dimensions $//<![CDATA[ \begin{array}{l}n \times r\end{array} //]]>$, n being the degrees of freedom of the full order model and r being the number of samples or snapshots.

$//<![CDATA[ \begin{array}{l}u_{snap}=[\overrightarrow{u_1} \space \overrightarrow{u_2} \space \overrightarrow{u_3} \space \overrightarrow{u_4} \space ...]_{n \times r }\end{array} //]]>$

The next step is to obtain the projection matrix by first computing the eigenvectors of $//<![CDATA[ \begin{array}{l}u^T_{snap} u_{snap}\end{array} //]]>$, which forms the basis for the reduced system. Normally the singular values of this matrix are computed, however, $//<![CDATA[ \begin{array}{l}u^T_{snap} u_{snap}\end{array} //]]>$ being a real symmetric matrix with non-negative eigenvalues the eigenvectors and singular vectors coincide.

$//<![CDATA[ \begin{array}{l}[basis]_{r \times r}=eig.vect. (u^T_{snap}u_{snap})\end{array} //]]>$

The projection matrix is obtained by multiplying the snapshot matrix with the basis.

$//<![CDATA[ \begin{array}{l}[V]_{n \times r}= u_{snap}basis\end{array} //]]>$

The projection step is performed as already illustrated in Figure 1.

$//<![CDATA[ \begin{array}{l}[K_r]_{r \times r}= V^TKV\end{array} //]]>$

$//<![CDATA[ \begin{array}{l}[M_r]_{r \times r}= V^TMV\end{array} //]]>$

$//<![CDATA[ \begin{array}{l}[f_r]_{r \times 1}= V^Tf\end{array} //]]>$

Krylov-Galerkin projection

The projection matrix is formed by applying the second-order Krylov subspace method. For this for each sampling frequency, three basis vectors are formed, which leads to the dimensions $//<![CDATA[ \begin{array}{l}n \times 3r\end{array} //]]>$.

$//<![CDATA[ \begin{array}{l}basis=[\overrightarrow{b_1} \space \overrightarrow{Ab_1} \space \overrightarrow{AAb_1} \space \overrightarrow{b_2} \space \overrightarrow{Ab_2} \space \overrightarrow{AAb_2} \space ...]_{n \times 3r}\end{array} //]]>$

with:

$//<![CDATA[ \begin{array}{l}K_{dyn}(\omega_i) \overrightarrow{b_i}=f\end{array} //]]>$

$//<![CDATA[ \begin{array}{l}K_{dyn}(\omega_i) \overrightarrow{Ab_i}=- \frac{\partial K_{dyn}}{\partial \omega} (\omega_i) \overrightarrow{b_i}\end{array} //]]>$

$//<![CDATA[ \begin{array}{l}K_{dyn}(\omega_i) \overrightarrow{AAb_i}=- \frac{\partial K_{dyn}}{\partial \omega} (\omega_i) \overrightarrow{Ab_i}- \frac{1}{2} \frac{\partial^2 K_{dyn}}{\partial^2 \omega} (\omega_i) \overrightarrow{b_i}\end{array} //]]>$

As a last step before the projection, an orthogonalization step is performed.

$//<![CDATA[ \begin{array}{l}[[V]_{n \times 3r} , \mathtt{\sim} ]=QR(basis)\end{array} //]]>$

The projection step is performed the same way as in the POD method.

$//<![CDATA[ \begin{array}{l}[K_r]_{3r \times 3r}= V^TKV\end{array} //]]>$
$//<![CDATA[ \begin{array}{l}[M_r]_{3r \times 3r}= V^TMV\end{array} //]]>$
$//<![CDATA[ \begin{array}{l}[f_r]_{3r \times 1}= V^Tf\end{array} //]]>$

The main difference to the POD is how the projection matrix is constructed. For each sampling frequency, three basis vectors are formed. In addition to the displacements, first and second derivatives of the dynamic stiffness matrix are taken into account and therefore try to match the moments of the forced response vector. [2]

Benchmark case

The system of the benchmark case is a cantilever beam with the dimensions $//<![CDATA[ \begin{array}{l}l=0.8\end{array} //]]>$ (longitudinal-direction), $//<![CDATA[ \begin{array}{l}w=0.01\end{array} //]]>$ (height) and $//<![CDATA[ \begin{array}{l}b=1.00\end{array} //]]>$. The material has a Young's modulus of $//<![CDATA[ \begin{array}{l}2.1\cdot 10^1^1\end{array} //]]>$, a density of $//<![CDATA[ \begin{array}{l}7860\end{array} //]]>$ and a poisson ratio of $//<![CDATA[ \begin{array}{l}0.3\end{array} //]]>$. The beam is discretized using 4 node quadrilateral elements in plane stress action. 320 elements in x-direction and 4 elements in y-direction are used, which can be considered overly fine discretized.

This cantilever was used for tuning the different reduced-order models and comparing their performance when it comes to accuracy and speedup:

For the optimization of the dynamic properties of the system, a mass-spring system was added at the tip of the cantilever:

Tuning the reduced-order models

The following figure shows the tip displacement of the cantilever beam over a frequency band from 0.1-6900 rad/s using the full order model (FOM).

Figure 2: Tip displacement FOM

As can be seen from the figure above the beam has 5 resonance modes and 5 antiresonances in the studied frequency band.

In the following, reduced-order models are constructed trying to match the response function of the FOM as accurate as needed for the optimization. The two influence parameters for constructing the reduced-order model are the number of sampling points and their position or sampling frequency. A linear spacing of the sampling points is compared to using the resonances and antiresonances for both the POD and the Krylov-Galerkin projection, which leads to four different possibilities to construct the reduced-order model:

• POD with linear spaced samples
• POD with resonance and antiresonance frequencies
• Krylov-Galerkin projection with linear spaced samples
• Krylov-Galerkin projection with resonance and antiresonance frequencies

The accuracy and time savings of the methods are compared to the full order model using the following measures:

$//<![CDATA[ \begin{array}{l}error=\frac{||\frac{w_{FOM}-w_{ROM}}{w_{FOM}}||_2}{n_{evaluations}}\end{array} //]]>$

$//<![CDATA[ \begin{array}{l}speedup=\frac{Time_{FOM}}{Time_{MOR}}\end{array} //]]>$

The error is therefore the error mean of all evaluation points in the full frequency band. The speedup is the ratio between the calculation time of the full order model and the reduced-order model.

Tuning process

The following images show the development of the error and the response function for the POD method with linear spaced sampling points. The sampling points are marked with red dashed lines. At those points, the reduced-order model always yields the best accuracy. It can be seen that for 3 sampling large deviations occur in the whole frequency band. 5 points lead to a much better matching for the frequencies above 2000 rad/s. If 7 points are used only around the frequency of 500 rad/s still too large deviations arise. When using 8 linearly spaced sampling points the FOM and the reduced-order model are nearly indistinguishable.

Figure 3: Tuning of the POD with linearly spaced sampling points

Comparison of the four applied strategies

The following plots show the speedup, which is the ratio between the computation time of the FOM and the ROM for different dimensions of the reduced model, and the relative approximation errors. It can be clearly seen that POD outperforms the Krylov-Galerkin projection with a speedup of 3.0-3.5 in comparison with a speedup of around 2.2. Above nine sampling points, there is a drop in the performance for the POD.

In general, the computation time of the ROM contains two major steps:

• Constructing the ROM
• Evaluation of the ROM 

Constructing the ROM takes around 60 % of the total computation time of the reduced-order model and evaluation roughly 40 % of the total time.

To ensure accurate results with the reduced model, an accuracy of less than 1% is expected. In the following figure, it can be seen that the Krylov-Galerkin projection needs at least a dimensionality of nine or 12 and the POD at least eight sampling points to ensure the desired accuracy. 

Taking speedup and accuracy into account, the best candidate for the optimization is the POD with eight linearly spaced samples.

Figure 4: Comparison of the MOR strategies

Optimization

Optimization problem formulation

The following figure shows the response of the system described in the Benchmark case without the mass-spring system.

Figure 5: System response before optimization

Now the local resonator is added and certain dynamic properties are optimized. The design variables for the optimization are the mass of the local resonator $//<![CDATA[ \begin{array}{l}m\end{array} //]]>$ and the exponent of the stiffness of the local resonator $//<![CDATA[ \begin{array}{l}exp_k\end{array} //]]>$. It is needed to take the exponent of the stiffnes as a variable instead of the stiffness to make sure that the values of the design variables are of the same scale, which leads to good convergence behaviour of the optimization algorithm. As lower and upper bounds of $//<![CDATA[ \begin{array}{l}m\end{array} //]]>$ approximately 5% and 15% of the mass of the beam are used. This leads to a lower bound of $//<![CDATA[ \begin{array}{l}m \geq \ 3\end{array} //]]>$ and a upper bound of $//<![CDATA[ \begin{array}{l}m \leq \ 10\end{array} //]]>$. The lower bound of $//<![CDATA[ \begin{array}{l}exp_k\end{array} //]]>$ is set to $//<![CDATA[ \begin{array}{l}2\end{array} //]]>$ which results in a stiffness of $//<![CDATA[ \begin{array}{l}k=10^2\end{array} //]]>$ and the upper bound of $//<![CDATA[ \begin{array}{l}exp_k\end{array} //]]>$ is set to $//<![CDATA[ \begin{array}{l}9\end{array} //]]>$ which leads to a stiffness of $//<![CDATA[ \begin{array}{l}k=10^9\end{array} //]]>$.

In the following, three different objectives are compared. The first two minimize the maximum deformation of the beam in the section 0-1000 rad/s and 4000-6000 rad/s. Since the max function is used the objective functions is not smooth in the design space. The third objective minimizes the fifth resonance peak at around 4700 rad/s. Therefore the range of interest is set to 4600-4800 rad/s and the minimization of the area is done by summing up the Euclidian norm of all points in the range of interest.

The system is optimized with a gradient-based algorithm. fmincon of MatLab is used which has the interior-point-algorithm as a default. The interior-point algorithm is capable of solving constrained optimization problems.

In the following the optimization problem is summarized:

Objectives:

• • $//<![CDATA[ \begin{array}{l}min \space f=max(|w_\omega|), \space \space 0 \space rad/s \leq \ \omega \leq \ 1000 \space rad/s\end{array} //]]>$
  • $//<![CDATA[ \begin{array}{l}min \space f=max(|w_\omega|), \space \space 4000 \space rad/s \leq \ \omega \leq \ 6000 \space rad/s\end{array} //]]>$
  • $//<![CDATA[ \begin{array}{l}min \space f=||w_\omega||_2, \space \space 4600 \space rad/s \leq \ \omega \leq \ 4800 \space rad/s\end{array} //]]>$

Variables:

mass of local resonator $//<![CDATA[ \begin{array}{l}m\end{array} //]]>$ 

exponent of stiffness of local resonator $//<![CDATA[ \begin{array}{l}exp_k\end{array} //]]>$ 

Bounds: 

$//<![CDATA[ \begin{array}{l}0.05m_{beam } \approx 3 \leq \ m \leq \ 10 \approx 0.15m_b_e_a_m\end{array} //]]>$

$//<![CDATA[ \begin{array}{l}10^2 \leq \ k \leq \ 10^9\end{array} //]]>$ → $//<![CDATA[ \begin{array}{l}2 \leq \ exp_k \leq \ 9\end{array} //]]>$

Algorithm:

Gradient-based algorithm: fmincon of MatLab → interior-point-algorithm

Effect of local resonator on ROM

For the following optimization the best method identified in Comparison of the four applied strategies being the POD with 8 linear distributed sampling points is used. To ensure the desired accuracy, the relative approximation error was rechecked after adding the local resonator.

If for the optimization in the low-frequency range a local resonator with $//<![CDATA[ \begin{array}{l}m = 6\end{array} //]]>$ and $//<![CDATA[ \begin{array}{l}exp_k = 5\end{array} //]]>$ is added to the model (left image) large deviations again can be observed. For the objective $//<![CDATA[ \begin{array}{l}min \space f=max(|w_\omega|), \space \space 0 \space rad/s \leq \ \omega \leq \ 1000 \space rad/s\end{array} //]]>$ it was, therefore, necessary to add an additional sampling point at 500 rad/s (right image) to obtain the needed accuracy.

For the other objectives 8 linearly distributed sampling points were sufficient to achieve the necessary accurarcy.

Figure 6: Effect of local resonator on ROM

Optimization workflow

For each combination of design variables a new reduced-order model has to be constructed since the ROM can not deal with the changes of the parameters. The sampling points remain unchanged during the optimization steps.

This leads to the following workflow:

Figure 7: Optimization workflow

Objective 1 and 2: Max Response in frequency range 0-1000 rad/s and 4000-6000 rad/s

The following objectives are now tried to minimize.

$//<![CDATA[ \begin{array}{l}min \space f=max(|w_\omega|), \space \space 0 \space rad/s \leq \ \omega \leq \ 1000 \space rad/s\end{array} //]]>$

$//<![CDATA[ \begin{array}{l}min \space f=max(|w_\omega|), \space \space 4000 \space rad/s \leq \ \omega \leq \ 6000 \space rad/s\end{array} //]]>$

Since both objectives aim to minimize a maximum value in a certain range they can be considered non-smooth like it can be seen from the plots of the objective functions. 

The system response of the starting position for the optimization and the related plots comparing the FOM with MOR are shown. It can be seen that good agreement between the FOM and the ROM is always reached. The second row of plots are the found solutions of the optimization. The optimizer was clearly able to decrease the objective function values. The last row of the table shows the objective functions, where the global minima are marked with the white box. There x represents $//<![CDATA[ \begin{array}{l}exp_k\end{array} //]]>$, y represents $//<![CDATA[ \begin{array}{l}m\end{array} //]]>$ and z represents the objective $//<![CDATA[ \begin{array}{l}log_1_0(objective)\end{array} //]]>$, which is scaled with $//<![CDATA[ \begin{array}{l}log_1_0\end{array} //]]>$ for better visualization.

For the optimization of the objectives which minimize the maximum value of the displacement the starting eigenfrequency of the local resonator needs to be chosen in the range of the minimization, otherwise, no good solution was found. The plots of the objectives $//<![CDATA[ \begin{array}{l}min \space f=max(|w_\omega|), \space \space 0 \space rad/s \leq \ \omega \leq \ 1000 \space rad/s\end{array} //]]>$ and $//<![CDATA[ \begin{array}{l}min \space f=max(|w_\omega|), \space \space 4000 \space rad/s \leq \ \omega \leq \ 6000 \space rad/s\end{array} //]]>$ show a non-convex shape with many local minima and maxima as well as kinks. Because of the noisy objectives, the used gradient-based algorithm gets stuck in a local minimum and can't find a good solution when the eigenfrequency of the local resonator isn't in the range of interest. When the eigenfrequency of the local resonator is in the range of interest the optimization finds a better solution than before but in most cases, it is one of the local minima and not the global minimum. For such noisy objectives population-based algorithms would be necessary to achieve convergence towards the global minimum.

Objective 3: Norm of response in the range of 4600-4800 rad/s

If the following objective is minimized different characteristics can be observed.

$//<![CDATA[ \begin{array}{l}min \space f=||w_\omega||_2, \space \space 4600 \space rad/s \leq \ \omega \leq \ 4800 \space rad/s\end{array} //]]>$

The design space of the objective is much smoother and more suitable for gradient-based algorithms. The domain of the objective still has some kinks and local minima, where the algorithm can get stuck without finding the global minimum. In the plot, the starting point and the found solution are marked with red dots. Again the global minimum is marked with a white box. It can be seen that the optimized solution is again a local minimum. The algorithm shows a more stable behaviour compared to the other objectives since it converges to a good solution in a large range of starting values.

For the optimization the following starting position was used, which is clearly outside the range of interest:

$//<![CDATA[ \begin{array}{l}m = 5.75\end{array} //]]>$, $//<![CDATA[ \begin{array}{l}exp_k = 7.25\end{array} //]]>$,  $//<![CDATA[ \begin{array}{l}\omega_n = 1759\end{array} //]]>$, $//<![CDATA[ \begin{array}{l}objective = 2.5484e-04\end{array} //]]>$

Figure 8: Start of optimization 

The optimizer finds now the following solution, which is improving the objective function quite significantly. Without the local resonator a resonance peak at 4700 rad/s could be observed. After the optimization the local resonator has an eigenfrequency of $//<![CDATA[ \begin{array}{l}\omega_n = 4699\end{array} //]]>$, which leads to an antiresonance.

$//<![CDATA[ \begin{array}{l}m = 6.11\end{array} //]]>$, $//<![CDATA[ \begin{array}{l}exp_k = 8.13\end{array} //]]>$,  $//<![CDATA[ \begin{array}{l}\omega_n = 4699\end{array} //]]>$, $//<![CDATA[ \begin{array}{l}objective = 7.367480e-07\end{array} //]]>$

Figure 9: Found solution

The objective function looks more suitable for gradient-based algorithms, although still having different local minima where the algorithm can get stuck.

Figure 10: Objective function

Comparison with the FOM

In the following, the optimization of the objective $//<![CDATA[ \begin{array}{l}min \space f=||w_\omega||_2, \space \space 4600 \space rad/s \leq \ \omega \leq \ 4800 \space rad/s\end{array} //]]>$ using the reduced-order models is compared with the optimization using the FOM. This time also the best candidate of the Krylov-Galerkin projection is considered, which is the one with 4 linearly spaced sampling points leading to a dimensionality of the ROM of 12.

The same starting points as in the comparison above are taken and the following results are obtained:

It can be seen that the FOM and both ROMs lead to almost identical results.

Conclusion

Model order reduction using the Proper orthogonal decomposition (POD) and the Krylov-Galerkin projection were used for gradient-based optimization. Both methods are projection-based model order reduction techniques. They lead to significantly faster computations compared with the full order model while keeping the needed accuracy of the results. POD was able to reduce the computation time more than the Krylov-Galerkin projection for the studied benchmark case. The optimization of the reduced-order model leads to almost identical results as the full order model, although just requiring a fraction of the computation time.

Future work could focus on the usage of parametric model order reduction that is able to preserve the parameter dependency, thus allowing a variation of the parameters without the need to repeat the reduction step, which leads to an even larger reduction of the computation costs. 

References

[1]Chair of Structural Mechanics at Technical University of Munich https://www.cee.ed.tum.de/bm/forschung/forschungsgebiete/parametrische-modellreduktion/

[2] Ophem, Sjoerd van: Novel reduction techniques for exterior vibro-acoustic models and their use in model-based sensing and identification, KU Leuven, Dissertation, 2019

[3] Rodriguez Sanchez, Raul; Buchschmid, Martin; Müller, Gerhard: Model order reduction in structural dynamics, TU München, 2016

[4] Matlab package bm-fem developed by the Chair of Structural Mechanics at Technical University of Munich

[5] Euclidean norm from: https://en.wikipedia.org/wiki/Norm_(mathematics)#Euclidean_norm (12.02.2022)

[6] Li, Quhao; Sigmund, Ole; Jensen, Jakob Søndergaard; Aage, Niels: Reduced-order methods for dynamic problems in topology optimization: A comparative study, 2021