Convolutional neural networks are built by concatenating individual blocks that achieve different tasks. These building blocks are often referred to as the layers in a convolutional neural network. In this section, some of the most common types of these layers will be explained in terms of their structure, functionality, benefits and drawbacks.
This section is an excerpt from Convolutional Neural Networks
Convolutional Layer
The main task of the convolutional layer is to detect local conjunctions of features from the previous layer and mapping their appearance to a feature map. As a result of convolution in neuronal networks, the image is split into perceptrons, creating local receptive fields and finally compressing the perceptrons in feature maps of size m_2 \ \times \ m_3. Thus, this map stores the information where the feature occurs in the image and how well it corresponds to the filter. Hence, each filter is trained spatial in regard to the position in the volume it is applied to.
In each layer, there is a bank of m_1 filters. The number of how many filters are applied in one stage is equivalent to the depth of the volume of output feature maps. Each filter detects a particular feature at every location on the input. The output Y_i^{(l)} of layer l consists of m_1^{(l)} feature maps of size m_2^{(l)} \ \times \ m_3^{(l)}. The i^{th} feature map, denoted Y_i^{(l)}, is computed as
| (1) | Y_i^{(l)} = B_i^{(l)} + \sum_{j=1}^{m_1^{(l-1)}} K_{i,j}^{(l)} \ast Y_j^{(l-1)} |
where B_i^{(l)} is a bias matrix and K_{i,j}^{(l)} is the filter of size 2h_1^{(l)} + 1 \ \times \ 2h_2^{(l)} + 1 connecting the j^{th} feature map in layer (l-1) with i^{th} feature map in layer.
The result of staging these convolutional layers in conjunction with the following layers is that the information of the image is classified like in vision. That means that the pixels are assembled into edglets, edglets into motifs, motifs into parts, parts into objects, and objects into scenes.
Original version of the page created by Simon Pöcheim can be found here.
Non-Linearity Layer
Rectification Layer
A rectification layer in a convolutional neural network performs element-wise absolute value operation on the input volume (generally the activation volume). Let layer l be a rectification layer, it takes the activation volume Y_i^{(l-1)} from a non-linearity layer (l-1) and generates the rectified activation volume Y_i^{(l)}:
| Y_i^{(l)} = |Y_i^{(l-1)}| |
Similar to the non-linearity layer, the element-wise operation properties do not change the size of the input volume and therefore, these operations can be (and in many cases(1) including AlexNet(4) and GoogLeNet(5) are) merged into a single layer:
| Y_i^{(l)} = | f(Y_i^{(l-1)})| |
Regardless of the general simplicity of the operation, it plays a key role in the performance of the convolutional neural network by eliminating cancellation effects in subsequent layers. Particularly when an average pooling method is utilized, the negative values within the activation volume are prone to cancel out the positive activations, degrading the accuracy of the network significantly. Therefore, the rectification is named as a "crucial component" (2).
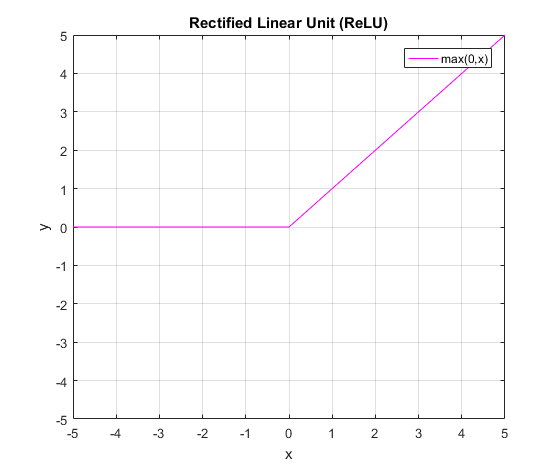
Rectified Linear Units (ReLU)
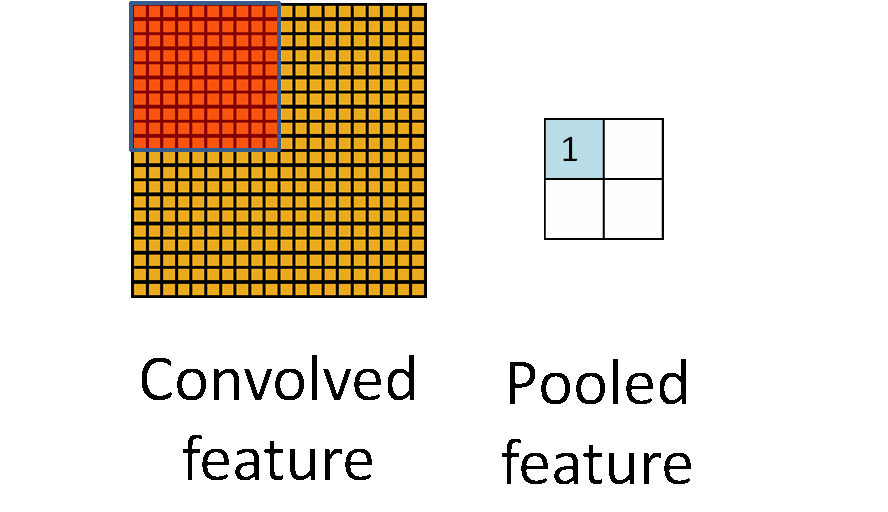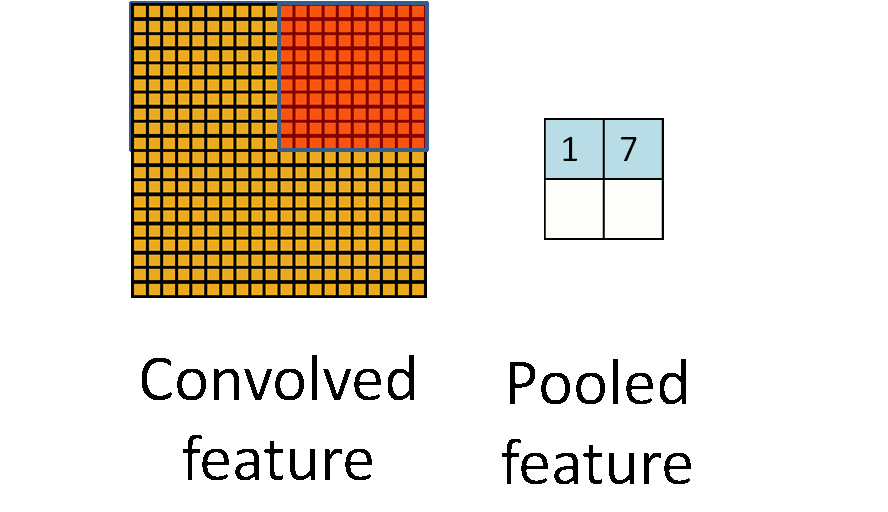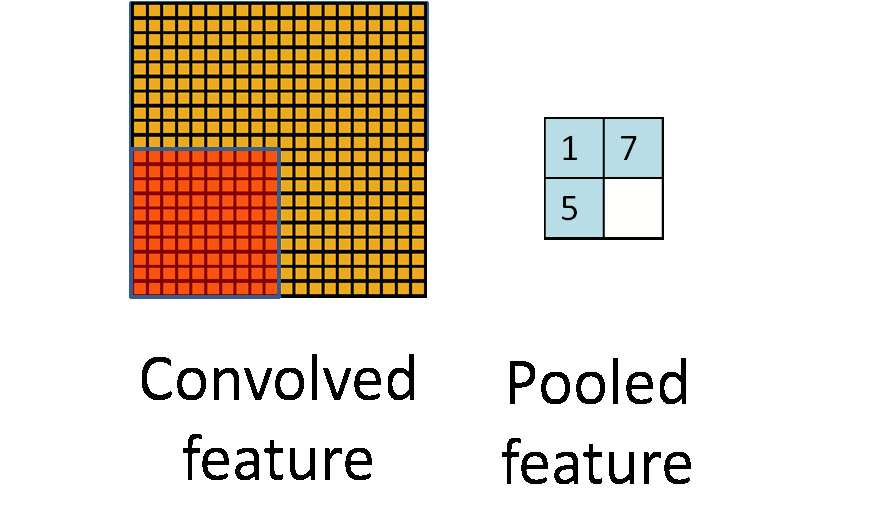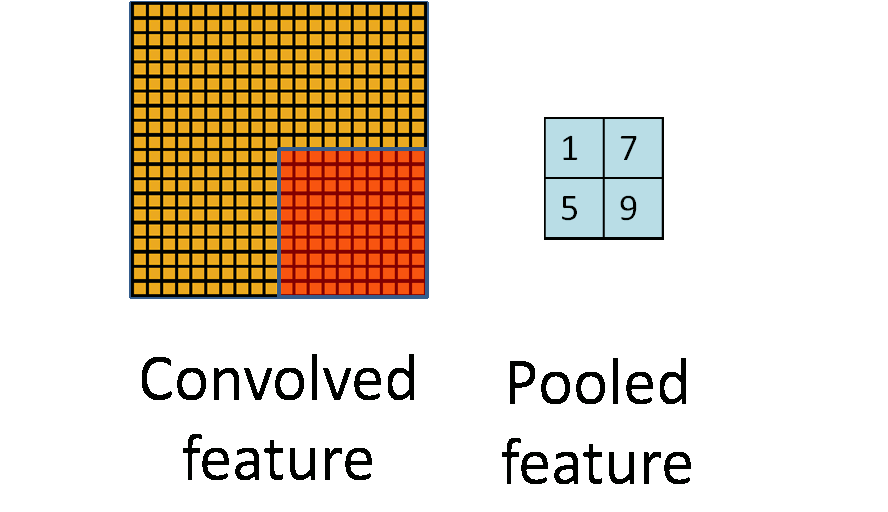
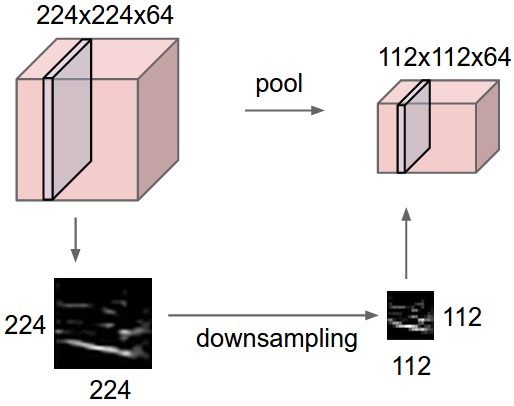
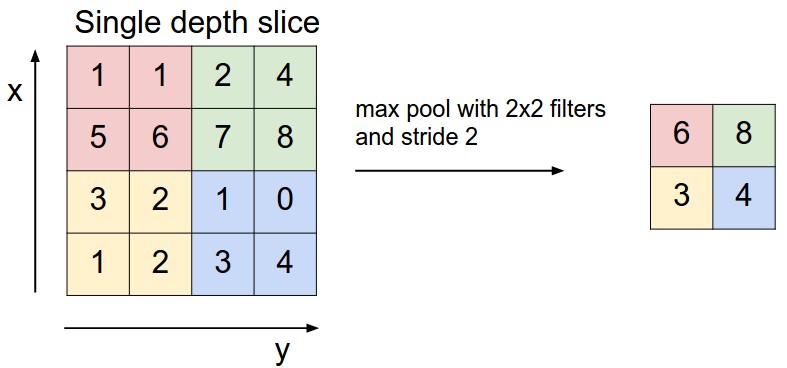
Pooling Layer
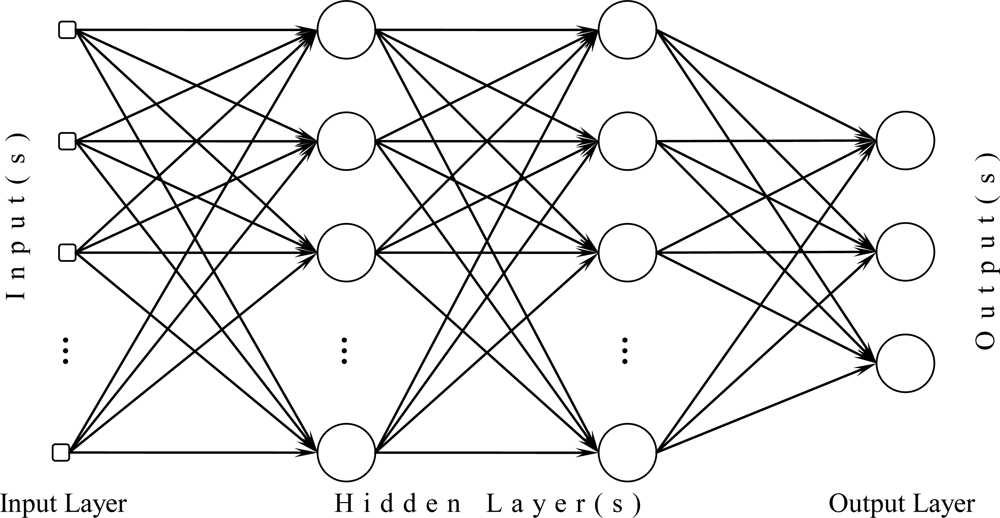
Fully Connected Layer
The goal of the complete fully connected structure is to tune the weight parameters w_{i,j}^{(l)} or w_{i,j,r,s}^{(l)} to create a stochastic likelihood representation of each class based on the activation maps generated by the concatenation of convolutional, non-linearity, rectification and pooling layers. Individual fully connected layers operate identically to the layers of the multilayer perceptron with the only exception being the input layer.
It is noteworthy that the function f once again represents the non-linearity, however, in a fully connected structure the non-linearity is built within the neurons and is not a seperate layer.
As a contradiction, according to Yann LeCun, there are no fully connected layers in a convolutional neural network and fully connected layers are in fact convolutional layers with a 1\times 1 convolution kernels (14). This is indeed true and a fully connected structure can be realized with convolutional layers which is becoming the rising trend in the research.
As an example; the AlexNet(4) generates an activation volume of 512\times7\times7 prior to its fully connected layers dimensioned with 4096, 4096, 1000 neurons respectively. The first layer can be replaced with a convolutional layer consisting of 4096 filters, each with a size of m_1 \times m_2 \times m_3 = 512 \times 7 \times 7 resulting in a 4096 \times 1 \times 1 output, which in fact is only a 1-dimensional vector of size 4096.
The architecture of AlexNet also depicting its dimensions including the fully connected structure as its last three layers.(Image source (4))
Subsequently, the second layer can be replaced with a convolutional layer consisting of 4096 filters again, each with a size of m_1 \times m_2 \times m_3 = 4096 \times 1\times 1 resulting in a 4096 \times 1 \times 1 output once again. Ultimately, the output layer can be replaced with a convolutional layer consisting of 1000 filters, each with a size of m_1 \times m_2 \times m_3 = 4096 \times 1\times 1 resulting in a 1000 \times 1 \times 1 output, which yields the classification result of the image among 1000 classes (13).
Literature
[1] Convolutional networks and applications in vision (2010, Yann LeCun, Koray Kavukcuoglu and Clement Farabet)
[2] What is the best multi-stage architecture for object recognition? (2009, Kevin Jarrett, Koray Kavukcuoglu, Marc'Aurelio Ranzato and Yann LeCun)
[3] Rectified Linear Units Improve Restricted Boltzmann Machines (2010, Vinod Nair and Geoffrey E. Hinton)
[4] ImageNet Classification with Deep Convolutional Neural Networks (2012, Alex Krizhevsky, Ilya Sutskever and Geoffrey E. Hinton)
[5] Going Deeper with Convolutions (2015, Christian Szegedy, Wei Liu, Yangqing Jia, Pierre Sermanet et al.)
[6] Deep Sparse Rectifier Neural Networks (2011, Xavier Glorot, Antoine Bordes and Yoshua Bengio)
[7] The CIFAR-10 dataset (2014, Alex Krizhevsky, Vinod Nair and Geoffrey E. Hinton)
[8] Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification (2015, Kaiming He, Xiangyu Zhang, Shaoqing Ren and Jian Sun)
[9] Evaluation of Pooling Operations in Convolutional Architectures for Object Recognition (2010, Dominik Scherer, Andreas Mueller and Sven Behnke)
[10] Fractional Max-Pooling (2014, Benjamin Graham)
[11] Striving for Simplicity: The All Convolutional Net (2014, Jost Tobias Springenberg, Alexey Dosovitskiy, Thomas Brox and Martin Riedmiller)
Weblinks
[12] http://ufldl.stanford.edu/tutorial/supervised/Pooling/ (Last visited: 21.01.2017)
[13] http://cs231n.github.io/convolutional-networks/#fc/ (Last visited: 21.01.2017)
[14] https://www.facebook.com/yann.lecun/posts/10152820758292143 (Last visited: 21.01.2017)
[15] http://iamaaditya.github.io/2016/03/one-by-one-convolution/ (Last visited: 21.01.2017)

3 Kommentare
Unbekannter Benutzer (ga29mit) sagt:
25. Januar 2017All the comments are SUGGESTIONS and are obviously highly subjective!
Form comments:
Wording comments:
Corrections:
image and mapping their appearance to a feature map
image and map their appearance to a feature map
neuronal network
neural network
can be (and in many cases(1) including AlexNet(4) and GoogLeNet(5) is)
can be (and in many cases(1) including AlexNet(4) and GoogLeNet(5) are)
Even though the general simplicity of the operation, it plays a key role in the performance
Regardless of the general simplicity of the operation, it plays a key role in the performance
Therefore the rectification is named as a "crucial component" (2).
Confusion:
Individual fully connected layers function identically (???) to the layers of the multilayer perceptron with the only exception being the input layer. (a verb is missing here)
Final remark:
Unbekannter Benutzer (ga69taq) sagt:
26. Januar 2017Thank you very much for the amazing contribution in such short time. I agree with almost all of your comments and they will be fixed, some points though i am unsure which way would work better so i would like to share them with you:
Form comments:
Wording comments:
Confusion:
Individual fully connected layers function identically (???) to the layers of the multilayer perceptron with the only exception being the input layer. (a verb is missing here): "Function" is the verb in that sentence not the name, as in "to function". I will switch the wording to "operate" in order to avoid confusion.
Everything else i agree and now have on my to do list. Again thank your very much for such a thorough and fast review. The largest problem is that now i'm under pressure that my reviews for other people will not be even half as thorough as yours .
.
As a last remark, when you select a text on viewing mode (i.e., not editing mode) a small message bubble appears which you can use to add inline comment to the page which i believe is extremely useful for reviewing.
Martin Knoche sagt:
31. Januar 2017Hi, first of all, it is really hard to find some suggestions as the second reviewer!
Regarding the language It sounds very good for me. I didn´t find any passage which I could correct or misunderstand.
The only thing I would suggest on your article is, that you could mention that there exist more Layers than all the Layers you mentioned. Like for example, DropOut Layer or BatchNormalization Layers. This is just a suggestion, but in my oppinion this will help beginners. They will see that this article is about the common layers but there will be more layers existing in common toolkits. You can also link these two other layers to the sections in the advanced level.
All in all a very good article!