Jonas Holtmann, summer semester 2016
“A wave […] is a collective bulk disturbance in which what happens at any given position is a delayed response to the disturbance at adjacent points.” [1]
Waves can be divided in two main categories. Firstly mechanical or elastic waves which propagate through a medium and secondly the electromagnetic wave which does not require a propagation medium and can therefore exist in vacuum. This article deals with the electromagnetic waves and their use in non-destructive testing. For elastic waves see Elastic waves.
Definition
Electromagnetic waves can be fully described by the Maxwell equations. They link the electric component of the wave with its magnetic component. The first equation links the electric charge \rho with the electric field E. The second equation links, similar to the first equation, the magnetic field with the magnetic charge. Up to date no magnetic charge was discovered. Therefore, there is no source and the term becomes zero. The third equation explains how electric field lines cover an area which is penetrated by a time varying magnetic field. It therefore connects the electric field E with the change rate of the magnetic field. The fourth equation describes how the magnetic field lines cover an area around a current flow or displacement current. [2]
The four Maxwell equations read as follows:
\oint_A E_n\ dA = \frac {1}{\varepsilon_0} q_i \qquad (1st Maxwell equation / Gauss's law)
\oint_A B_n\ dA = 0 \qquad (2nd Maxwell equation / Gauss's law for magnetism)
oint_C E\ dl = - \int_A \frac{\partial B_n} {\partial t} dA \qquad (3rd Maxwell equation / Faraday's law)
\oint_C B\ dl = \mu_o (I + I_V) \qquad with I_V = \varepsilon_0 \int_A \frac{\partial E_n} {\partial t} dA \qquad (4th Maxwell equation / Ampère's circuital law) [2]
with:
E_n = electric field
\varepsilon_0 = permittivity of free space
B_n = magnetic field
q_i = enclosed electric charge
\mu_0 = permeability of free space
I = electric current
and:
A = integration area
C = integration path
By mathematical transformation the wave equation for the electric wave can be derived from the Maxwell equations.
\Delta E - \varepsilon \varepsilon_0 \mu_0 \frac{\partial^2 E}{\partial t^2} = 0 \qquad Wave equation for electromagnetic waves [4]
The solutions to this differential equation describe all harmonic oscillating waves. By setting specific boundary conditions concrete electromagnetic waves can be described.
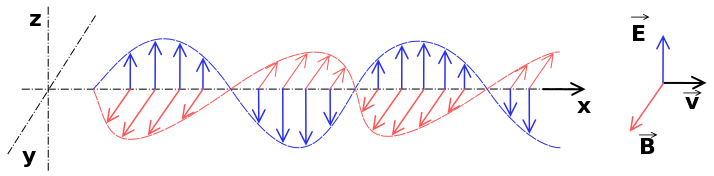
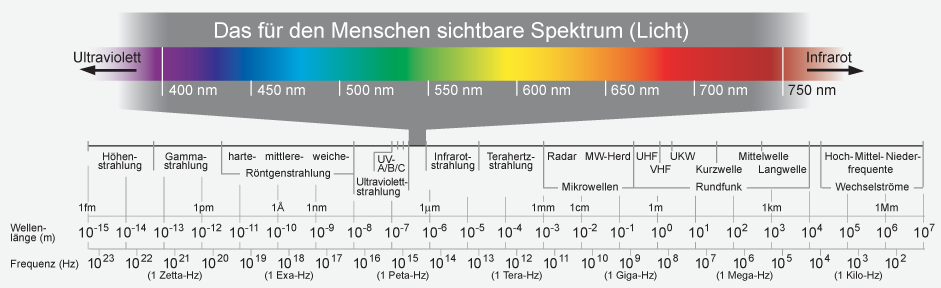
Figure 1: Illustration of an electromagnetic wave [3] By SuperManu - Self, based on Image:Onde electromagnetique.png, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=2107870 | Figure 2: Electromagnetic spectrum „Spektrum v8“ by Horst Frank - SVG-Version: http://www.zeitmaschinisten.com/svg/Spektrum.svg. Licensed under CC BY-SA 3.0 Wikimedia Commons - https://commons.wikimedia.org/wiki/File:Spektrum_v8.png#/media/File:Spektrum_v8.png |
Important quantities of waves
Wave speed: The wave speed in vacuum is c = 299.792.458 m/s. In matter it depends on the relative permeability and relative permittivity of the object and the frequency of the wave. [5]
Wavelength: The distance between two neighbouring wave maxima. [2]
Frequency: The inverse of the time t for one complete cycle of an oscillating wave. The frequency f and the wavelength \lambda are linked by the wave speed in the following way: c = f * \lambda. [2] The electromagnetic spectrum with its corresponding frequency and wavelength are shown in Figure 2.
There are three possible types of interaction of an electromagnetic wave with matter:
Reflexion: The electromagnetic wave changes its direction in such a way that it returns into the medium it originated from. The angle of incidence equals the angle of reflection (Figure 4). [5]
Absorption: The electromagnetic wave interacts with matter in such a way that its energy is transformed into another energy form, e.g. into heat. [6]
Transmission: The electromagnetic wave travels through the medium. Normally it changes its direction (refraction) depending on the indices of refraction. [6] The angle of incidence and the angle of refraction are linked by the formula of Snellius \frac {sin (\alpha_1)}{sin (\alpha_2)} = \frac{c_1}{c_2} . [7] Figure 4 illustrates the interaction of an electromagnetic wave at an interface.
Intensity: The mean power travelling through an area which is perpendicular to the wave direction. [2]
Polarization: If the electric part of the wave has only one swinging plane the wave is called linear polarized. [8]
| Figure 3: Illustration of the wavelength | Figure 4: Interaction of a wave at the interface of two materials [5]. |
Use in NDT applications
Radar: Uses electromagnetic waves with a frequency between 10 MHz and 2.5 GHz. Properties of the tested object, such as its relative permeability and relative permittivity, can be derived by interpreting the reflection of the wave. [9]
Polarisation: The interaction of polarised electromagnetic waves with an object can provide information about the material properties, e.g. the absorption of light on carbon fibres differ, depending on the polarisation of the incident light. [10]
Visual inspection: DIN-EN 1330-10 defines the visual inspection as a testing method on the basis of electromagnetic waves in the visual bandwidth. It is therefore a valid non-destructive testing method. [7]
Infrared Thermography: Uses the infrared spectrum of the electromagnetic bandwidth to obtain information about the radiation of the test object. [11] The infrared spectrum is bounded by the visible spectrum at approximately 700 nm and the terahertz spectrum at approximately 10 μm. The infrared thermography uses the characteristic of objects to radiate. Every object with a temperature above 0 K emits radiation in certain wavelengths. For the NDT the object can be excited e.g. by ultrasonic probes or light. This method is called active thermography. Another method uses the infrared radiation emitted by the object by itself. This is called passive thermography.
Figure 5: Exemplary radar system GSSI StructureScan Mini | Figure 6: Infrared-Thermography Detecting studwork structures in a house. © Dr. Jürgen Frick, MPA Universität Stuttgart. |
Literature
- Freegarde, T.: Introduction to the physics of waves. 2013.
- Tipler; et al.: Physik für Wissenschaftler und Ingenieure. 2015.
- SuperManu - Self, based on Image: Onde electromagnetique.png. CC BY-SA 3.0, Wikimedia. 2007.
- Zinth, W; Zinth, U: Optik. Lichtstrahlen - Wellen - Photonen. 2011.
- Schröder; et al.: Technische Optik. Grundlagen und Anwendungen. 2014.
- Beyerer; et al.: Automatische Sichtprüfung. Grundlagen, Methoden und Praxis der Bildgewinnung und Bildauswertung. 2012.
- Schiebold, K.: Zerstörungsfreie Werkstoffprüfung - Sichtprüfung. 2015.
- Gruyter, D: Mechanik - Wellen - Wärme. 2012.
- Jol, H. M. (Hg.): Ground penetrating radar theory and applications. 2009.
- Freitag, C.; Weber, R.; Graf, T.: Polarization dependence of laser interaction with carbon fibers and CFRP. In: Optics express 22 (2). 2014.
- Minkina, W.; Dudzik, S.: Infrared thermography. Errors and uncertainties. 2009.